Cours FONCTION EXPONENTIELLE
Exercice 1 Signe d’une expression
Déterminer, en fonction de 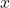 , le signe des fonction suivantes :
, le signe des fonction suivantes :
-
 définie sur
définie sur  par
par 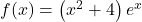 .
.
-
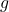 définie sur
définie sur  par
par 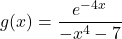 .
.
-
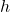 définie sur
définie sur  par
par 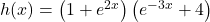 .
.
-
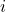 définie sur
définie sur  par
par 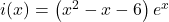 .
.
Correction Exercice 1
-
 définie sur
définie sur  par
par 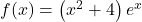 .
La fonction exponentielle est strictement positive sur
.
La fonction exponentielle est strictement positive sur  . Par conséquent, pour tout réel
. Par conséquent, pour tout réel 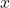 on a
on a 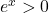 .
De plus, pour tout réel
.
De plus, pour tout réel 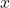 on a
on a 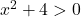 .
Ainsi
.
Ainsi 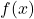 est strictement positif sur
est strictement positif sur  .
.
-
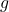 définie sur
définie sur  par
par 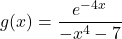 .
La fonction exponentielle est strictement positive sur
.
La fonction exponentielle est strictement positive sur  . Par conséquent, pour tout réel
. Par conséquent, pour tout réel 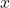 on a
on a 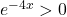 .
De plus, pour tout réel
.
De plus, pour tout réel 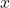 on a
on a 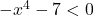 .
Ainsi
.
Ainsi 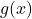 est strictement négatif sur
est strictement négatif sur  .
.
-
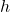 définie sur
définie sur  par
par 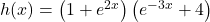 .
La fonction exponentielle est strictement positive sur
.
La fonction exponentielle est strictement positive sur  . Par conséquent, pour tout réel
. Par conséquent, pour tout réel 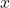 on a
on a 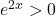 et
et 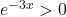 .
Donc
.
Donc 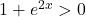 et
et 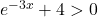 .
Ainsi
.
Ainsi 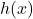 est strictement positif sur
est strictement positif sur  .
.
-
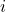 définie sur
définie sur  par
par 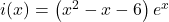 .
La fonction exponentielle est strictement positive sur
.
La fonction exponentielle est strictement positive sur  . Par conséquent, pour tout réel
. Par conséquent, pour tout réel 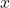 on a
on a 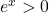 .
On étudie donc le signe de
.
On étudie donc le signe de 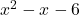 .
Il s’agit d’un polynôme du second degré.
.
Il s’agit d’un polynôme du second degré.
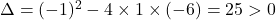 .
Il possède deux racines réelles :
.
Il possède deux racines réelles :
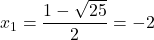 et
et 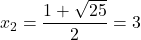 Le coefficient principal est
Le coefficient principal est 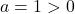 .
Ainsi
.
Ainsi 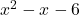 est positif sur
est positif sur ![Rendered by QuickLaTeX.com ]-\infty;-2]\cup[3;+\infty[](https://spe-maths.fr/wp-content/ql-cache/quicklatex.com-502280c678553961170b927a229f05fe_l3.png) et négatif sur
et négatif sur ![Rendered by QuickLaTeX.com [-2;3]](https://spe-maths.fr/wp-content/ql-cache/quicklatex.com-5f3c1ff2a5c09cb1970daf48aeb32b18_l3.png) .
Par conséquent :
.
Par conséquent :
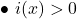 sur
sur ![Rendered by QuickLaTeX.com ]-\infty;-2[\cup]3;+\infty[](https://spe-maths.fr/wp-content/ql-cache/quicklatex.com-99c616bd5d6944577033212cc312606c_l3.png) ;
;
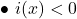 sur
sur ![Rendered by QuickLaTeX.com ]-2;3[](https://spe-maths.fr/wp-content/ql-cache/quicklatex.com-84a19a88a8954426254281efa7a2b7f3_l3.png) ;
;
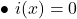 si
si 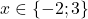 .
.