On calcule, à la calculatrice, $u_n$ pour les premières valeurs de $n$.
$\begin{array}{|*{11}{>{\ca}p{0.8cm}|}}
\hline
n &0 &1 &2 &3 &4 &5 &6 &7 &8 & \dots\\\hline
u_n &1 &1,8&2,44 &2,95 &3,36 &3,69 &3,95 &4,16 &4,33 & \dots \\\hline
\end{array}$
$\begin{array}{|*{11}{>{\ca}p{0.8cm}|}}\hline
n &\dots &20 & 21 & 22 & 23 & 24 & 25 & 26 & 27 & 28 \\\hline
u_n &\dots &4,95 &4,96 &4,97 &4,976 &4,981 &4,985 &4,988 &4,990 &4,992 \\\hline
\end{array}$
La suite $\left(u_n\right)$ semble croissante et semble converger vers 5.
- Soit $\mathcal{P_n}$ la propriété $u_n = 5 - 4 \times 0,8^n$.
Initialisation : Pour $n = 0$, $u_0 = 1$ et $5 - 4\times 0,8^{0} = 5 - 4 = 1$. Donc la propriété $\mathcal{P_0}$ est vérifiée.
Hérédité : Soit $n$ un entier naturel quelconque.
On suppose que la propriété est vraie pour le rang $n$ c'est-à-dire $u_n=5-4\times 0,8^n$ $($ c'est l'hypothèse de récurrence$)$, et on veut démontrer qu'elle est encore vraie pour le rang $n+1$.
$u_{n+1} = 0,8 u_n +1$. Or, d'après l'hypothèse de récurrence $u_n=5-4\times 0,8^{n}$; donc:
$u_{n+1} = 0,8 \left ( 5 - 4\times 0,8^n \right ) +1
= 0,8\times 5 - 4 \times 0,8^{n+1} +1
= 4 - 4 \times 0,8^{n+1} +1
= 5 - 4 \times 0,8^{n+1}$
Donc la propriété est vraie au rang $n+1$. La propriété $\mathcal{P_n}$ est donc héréditaire pour tout $n$.
Conclusion : La propriété est vraie pour $n = 0$. Elle est héréditaire à partir du rang 0.
Donc, d'après le principe de récurrence, la propriété est vraie pour tout entier naturel $n$.
- $u_{n+1}-u_n=\left ( 5-4\times 0,8^{n+1}\right ) - \left ( 5-4\times 0,8^{n}\right )= 5-4\times 0,8^{n+1} - 5+4\times 0,8^{n}= 4\times 0,8^n \left (1-0,8\right )\\
\phantom{u_{n+1}-u_n}= 4\times 0,8^n \times 0,2 > 0$
Pour tout $n$, on a démontré que $u_{n+1} > u_n$ donc la suite $(u_n)$ est croissante.
$-1<0,8 < 1$ donc la suite géométrique $(0,8^n)$ de raison 0,8 converge vers 0.
$\lim\limits_{n \to +\infty} 0,8^n=0$, et $\lim\limits_{n \to+\infty} 4\times 0,8^n=0$ donc $ \lim\limits_{n \to +\infty} 5-4\times 0,8^n=5$.
|
 Sens de variations d’une suite à l’aide du signe de
Sens de variations d’une suite à l’aide du signe de 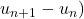
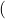 Sens de variations d’une suite à l’aide du signe de
Sens de variations d’une suite à l’aide du signe de 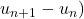
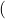 Sens de variations d’une suite à l’aide de
Sens de variations d’une suite à l’aide de 
 Sens de variations d’une suite définie par une fonction
Sens de variations d’une suite définie par une fonction 
 Sens de variations d’une suite définie par récurrence
Sens de variations d’une suite définie par récurrence 
 Suite auxiliaire géométrique
Suite auxiliaire géométrique