Limites de fonctions
Exercice 1 (Opérations sur les limites)
Calculer dans chacun des cas la limite demandée.
- $\lim\limits_{x \rightarrow 2^+} \frac{1}{x - 2} \quad \quad$ : Réponse $\color{red}{+\infty}$
$\quad$
- $\lim\limits_{x \rightarrow 1^+} \left(\left(5+\frac{1}{\sqrt{x-1}}\right) (2x+3)\right) \quad \quad$ : Réponse $\color{red}{+\infty}$
- $\lim\limits_{x \rightarrow 4^+} \frac{1-x}{x-4} \quad \quad$ : Réponse $\color{red}{-\infty}$
$\quad$
- $\lim\limits_{x \rightarrow 3^-} \frac{x^3-1}{3-x} \quad \quad$ : Réponse $\color{red}{+\infty}$
$\quad$
- $\lim\limits_{x \rightarrow +\infty} \frac{\sqrt{x+1}+\sqrt{x}}{x} \quad \quad$ : Réponse $\color{red}{0}$
- $\lim\limits_{x \rightarrow +\infty} \frac{x+1}{\sqrt{x}} \quad \quad$ : Réponse $\color{red}{+\infty}$
$\quad$
- $\lim\limits_{x \rightarrow -1^-} \frac{3x^2-5}{3x+3}\quad \quad$ : Réponse $\color{red}{+\infty}$
Pour des exercices corrigés type bac sur les fonctions , Cliquez ici |
Corrigé de l'exercice 1
- $\lim\limits_{x \rightarrow 2^+} (x -2) = 0^+$ donc $\lim\limits_{x \rightarrow 2^+} \frac{1}{x - 2} = +\infty$
- $\lim\limits_{x \rightarrow 1^+} \frac{1}{\sqrt{x-1}} =+\infty$
De plus $\lim\limits_{x \rightarrow 1^+} (2x+3) = 5$.
Par conséquent $\lim\limits_{x \rightarrow 1^+} \left(\left(5+\frac{1}{\sqrt{x-1}}\right) (2x+3)\right) = +\infty$
- $\lim\limits_{x \rightarrow 4^+} (1-x) = -3$ et $\lim\limits_{x \rightarrow 4^+} (x-4) = 0^+$ donc
$\lim\limits_{x \rightarrow 4^+} \frac{1-x}{x-4} = -\infty$
- $\lim\limits_{x \rightarrow 3^-}(x^3-1) = 26$ et $\lim\limits_{x \rightarrow 3^-} (3-x) = 0^+$ donc
$\lim\limits_{x \rightarrow 3^-} \frac{x^3-1}{3-x} = +\infty$
- $\frac{\sqrt{x+1} - \sqrt{x} }{x} = \sqrt{\frac{1}{x}+\frac{1}{x^2}}-\frac{1}{\sqrt{x}}$.
Or $\lim\limits_{x \rightarrow +\infty} \frac{1}{x} =\lim\limits_{x \rightarrow +\infty} \frac{1}{x^2} = 0$ et $\lim\limits_{x \rightarrow +\infty} \frac{1}{\sqrt{x}} = 0$
Donc $\lim\limits_{x \rightarrow +\infty} \frac{\sqrt{x+1} - \sqrt{x}}{x} = 0$
- $\frac{x+1}{\sqrt{x}} = \frac{x}{\sqrt{x}} + \frac{1}{\sqrt{x}}= \sqrt{x}+\frac{1}{\sqrt{x}}$.
Or $\lim\limits_{x \rightarrow +\infty} \sqrt{x}=+\infty$ et $\lim\limits_{x \rightarrow +\infty} \frac{1}{\sqrt{x}}=0$ Par conséquent $\lim\limits_{x \rightarrow +\infty} \frac{x+1}{\sqrt{x}}=+\infty$
- $\lim\limits_{x \rightarrow -1^-}(3x^2-5)= -2$ et $\lim\limits_{x \rightarrow -1^-} (3x + 3) = 0^-$
Donc $\lim\limits_{x \rightarrow -2^-} \frac{3x^2-5}{3x +3} = +\infty$
|
Exercice 2
A-Déterminer la limite à gauche et la limite à droite des fonctions suivantes en a.
1. 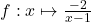 ;
; 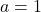 Réponse
Réponse 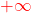 et
et 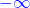
2. 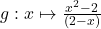 ;
; 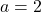 Réponse
Réponse  et
et 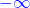
3. 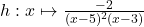 ;
; 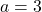 Réponse
Réponse  et
et 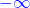
4. 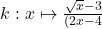 ;
; 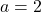 Réponse
Réponse  et
et 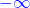
5.  ;
; 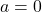 Réponse
Réponse  et
et 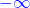
6. 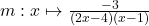 ;
; 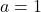 Réponse
Réponse  et
et 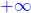
7. 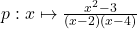 ;
; 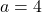 Réponse
Réponse  et
et 
B- Déterminer la limite des fonctions suivantes en a. « Forme indéterminée 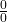 «
«
1. 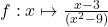 ;
; 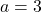 Réponse
Réponse 
2.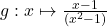 ;
; 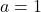 Réponse
Réponse 
3. 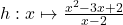 ;
; 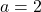 Réponse
Réponse 
4. 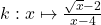 ;
; 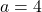 Réponse
Réponse 
Pour les limites suivantes utiliser la dérivation
5.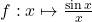 ;
; 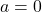 Réponse
Réponse 
6. 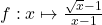 ;
; 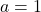 Réponse
Réponse 
7. 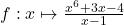 ;
; 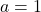 Réponse
Réponse 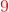
8. 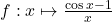 ;
; 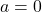 Réponse
Réponse 
Corrigé de l'exercice 2
A. Limite du type " $\color{blue} {\frac{\alpha}{0}}$" avec $\alpha \neq 0$
1. $\lim\limits_{x \to 1^-} (x-1) = 0^-$ donc $\lim\limits_{x \to 1^+} \frac{-2}{x - 1}=\color{red}{+\infty}$
et comme $\lim\limits_{x \to 1^+} (x-1) = 0^+$ alors $\lim\limits_{x \to 1^+} \frac{-2}{x - 1}=\color{blue}{-\infty}$
2. $\lim\limits_{x \to 2} (x^2-2) = 2$ et $\lim\limits_{x \to 2^-}(2-x)=0^+$ donc $\lim\limits_{x \to 2^-}\frac{x^2-2}{2 - x}=\color{red}{+\infty}$
et comme $\lim\limits_{x \to 2^+}(2-x)=0^-$ alors $\lim\limits_{x \to 2^+}\frac{x^2-2}{2 - x}=\color{blue}{-\infty}$
3. $\lim\limits_{x \to 3^-} (x - 5)^2(x - 3) = 0^-$ donc $\lim\limits_{x \to 3^+}\frac{-2}{(x - 5)^2(x - 3)}=\color{red}{+\infty}$
et $\lim\limits_{x \to 3^+} \frac{-2}{(x - 5)^2(x - 3)}=\color{blue}{-\infty}$
4. $\lim\limits_{x \to 2} (\sqrt{x} - 3) = \sqrt{2}-3 < 0$ et $\lim\limits_{x \to 2^-}(2x - 4)=0^-$ donc $\lim\limits_{x \to 2^-}\frac{\sqrt{x} - 3}{2x - 4}=\color{red}{+\infty}$ et $\lim\limits_{x \to 2^+}\frac{\sqrt{x} - 3}{2x - 4}=\color{blue}{-\infty}$
5. $\lim\limits_{x \to 0^-} x(x - 5)^2 = 0^-$ donc $\lim\limits_{x \to 0^-}\frac{-2}{x(x - 5)^2}=\color{red}{+\infty}$
et $\lim\limits_{x \to 0^+} \frac{-2}{x(x - 5)^2}=\color{blue}{-\infty}$
6. $\lim\limits_{x \to 1^-} (2x - 4)(x-1) = 0^+$ donc $\lim\limits_{x \to 1^-} \frac{ - 3}{(2x - 4)(x-1)}=\color{red}{-\infty}$
d'autre part $\lim\limits_{x \to 1^+}(2x - 4)(x-1)=0^-$ par conséquent $\lim\limits_{x \to 1^+} \frac{ - 3}{(2x - 4)(x-1)}=\color{blue}{+\infty}$
7. $\lim\limits_{x \to 4}(x^2- 3)=15$ et $\lim\limits_{x \to 4^-} ((x - 2)(x-4) = 0^-$ donc $\lim\limits_{x \to 4^-} \frac{ x^2- 3}{(x - 2)(x-4)}=\color{red}{-\infty}$
et comme $\lim\limits_{x \to 4^+}(2x - 4)(x-1)=0^+$ alors $\lim\limits_{x \to 4^+}\frac{ x^2- 3}{(x - 2)(x-4)}=\color{blue}{+\infty}$
|
B. Forme indéterminée" $\color{blue} {\frac{0}{0}}$"
1. Pour $x \neq 3$ ona $f(x) = \frac{x-3}{x^2-9} = \frac{x-3}{(x-3)(x+3)} = \frac{1}{x+3}$ donc $\lim\limits_{x \to 3}f(x)=\lim\limits_{x \to 3}\frac{1}{x+3}=\color{red}{\frac{1}{6}}$
2. Pour $x \neq 1 $ on a $g(x) = \frac{x-1}{(x-1)(x+1)} = \frac{1}{x+1}$ donc $\lim\limits_{x \to 1}g(x)=\lim\limits_{x \to 1}\frac{1}{x+1}=\color{red}{\frac{1}{2}}$
3. Pour $x \neq 2 $ on a $h(x) = \frac{(x-1)(x-2)}{x-2} = x-1 $ donc $\lim\limits_{x \to 2}h(x)=\lim\limits_{x \to 2}(x-1)=\color{red}{1}$
4. Pour $x > 0 $ et $x \neq 4$ on a $k(x) = \frac{\sqrt{x}-2}{(\sqrt{x}- 2)(\sqrt{x}+ 2)} = \frac{1}{\sqrt{x}+ 2} $ donc $\lim\limits_{x \to 4}k(x)=\lim\limits_{x \to 4}\frac{1}{\sqrt{x}+ 2} =\color{red}{\frac{1}{4}}$
Pour les limites suivantes on utilise la définition de la dérivée de la fonction $f$ en $a$ : $$\lim\limits_{x \to a}\frac{f(x) - f(a)}{x - a}=f'(a)$$
5.$\frac{\sin{x}}{x }=\frac{\sin{x}-0}{x-0 }=\frac{f(x)-f(0)}{x-0 }$ où $f(x)=\sin{x}$
La fonction $f$ est dérivable sur $\mathbb R$ donc en $0$ et sa dérivée est donnée par $f'(x)=\cos{x}$; $f'(0)=1$
comme $f$ est dérivable en $0$ $\lim\limits_{x \to 0}\frac{\sin{x}}{x }=\lim\limits_{x \to 0}\frac{\sin{x} - \sin{0} }{x - 0}=f'(0)=\color{red}{1}$.
6.$\frac{\sqrt{x}-1}{x-1 }=\frac{f(x)-f(1)}{x-1 }$ où $f(x)=\sqrt{x}$.
La fonction $f$ est dérivable sur $[0,+\infty$ donc en $1$ et sa dérivée est donnée par $f'(x)=\frac{1}{2\sqrt{x}}$; $f'(1)=\frac{1}{2}$
comme $f$ est dérivable en $1$ $\lim\limits_{x \to 1}\frac{\sqrt{x}-1}{x -1}=f'(1)=\color{red}{\frac{1}{2}}$.
7.Si on pose $f(x)=x^6+3x$ on a alors $f(1) = 1^6+3 =4$ et donc $$\frac{x^6+3x-4}{x-1}=\frac{f(x)-f(1)}{x-1 }$$
La fonction $f$ est dérivable sur $\mathbb R$ donc en $1$ et sa dérivée est donnée par $f'(x)=6x^5+3$; $f'(1)=9$
comme $f$ est dérivable en $1$, $\lim\limits_{x \to 1}\frac{(x^6+3x)-4}{x-1 }=f'(1)=\color{red}{9}$.
8.$\frac{\cos{x}-1}{x }=\frac{f(x)-f(0)}{x-0 }$ où $f(x)=\cos{x}$.
La fonction $f$ est dérivable sur $\mathbb R$ donc en $0$ et sa dérivée est donnée par $f'(x)=-\sin{x}$; $f'(0)=0$
comme $f$ est dérivable en $0$ $\lim\limits_{x \to 0}\frac{\cos{x}-1}{x }=f'(0)=\color{red}{0}$.
|
Exercice 3 (Limites dans le tableau de variations)
On donne le tableau de variations d’une fonction  :
:
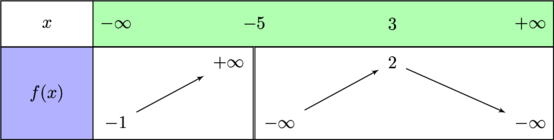
1) Déterminer les limites de  en
en  , en
, en 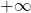 , en -5 à gauche et à droite.
, en -5 à gauche et à droite.
Corrigé de l'exercice 3
$\lim\limits_{x \to -\infty} f(x) = -1$
$\lim\limits_{x \to +\infty } f(x) = -\infty$
$\lim\limits_{x \to -5^-} f(x) = +\infty$
$\lim\limits_{x \to -5^+} f(x) = -\infty$
|
Exercice 4
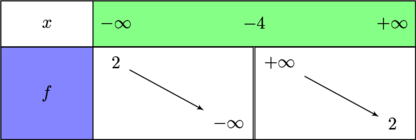
On connaît le tableau de variations d’une fonction  :
:
On sait de plus qu’il existe 2 réels  ,
, 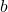 tels que
tels que  est définie sur
est définie sur 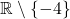 , par
, par 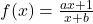 . Déterminer les valeurs de
. Déterminer les valeurs de  ,
, 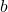 en justifiant.
en justifiant.
Corrigé de l'exercice 4
La fonction $f$ n'est pas définie en $x = -b$, donc $-b = -4$. Ainsi, $b = 4$.
Pour $x \neq 0$ on a $f(x) = \frac{ax+1}{x+b} = \frac{ax+1}{x+4} = \frac{ax(1+\frac{1}{ax})}{x(1+\frac{4}{x})} = \frac{a(1+\frac{1}{ax})}{(1+\frac{4}{x})}$. On en déduit les limites de $f$ en $ -\infty$ et $ +\infty$:
$\lim\limits_{x \to -\infty} f(x) = a$ et $\lim\limits_{x \to +\infty} f(x) = a $ et d'aprés le tableau de variation a= 2.
La fonction $f$ est donnée par $f(x)=\frac{2x+1}{x+4} $ |
Exercice 5 (asymptotes horizontales et verticales)
On a tracé ci-dessous la courbe d’une fonction  définie sur
définie sur 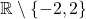 . Déterminer graphiquement les limites de
. Déterminer graphiquement les limites de  en
en  , en
, en 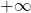 , en -2 et en 2 à droite et à gauche. Indiquer les asymptotes.
, en -2 et en 2 à droite et à gauche. Indiquer les asymptotes.
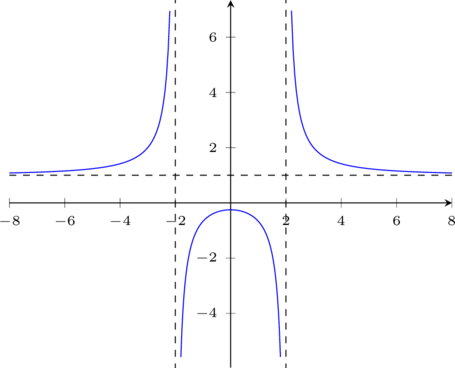
Corrigé de l'exercice 5
Asymptote horizontale d'équation $y=1$
- $\lim\limits_{x \to -\infty} f(x) = 1$
- $\lim\limits_{x \to +\infty } f(x) = 1$
Asymptotes verticales d'équations $x=-2$ et $x=2$
$\lim\limits_{x \to -2^-} f(x) = +\infty$
$\lim\limits_{x \to -2^+} f(x) = -\infty$
$\lim\limits_{x \to 2^-} f(x) = -\infty$
$\lim\limits_{x \to 2^+} f(x) = +\infty$
|
Exercice 6(QCM asymptotes)
Q1. Soit la fonction  définie sur
définie sur 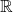 donnée par
donnée par 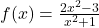 . La courbe
. La courbe 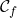 admet comme asymptote la droite d’équation :
admet comme asymptote la droite d’équation :
a. 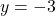 b.
b. 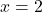 c.
c. 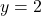 d.
d. 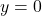
Q2. Soit la fonction 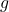 définie sur
définie sur 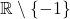 par
par 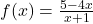 . La courbe
. La courbe 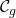 admet commes asymptotes :
admet commes asymptotes :
a. 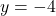 b.
b. 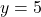 c.
c. 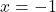 d.
d. 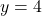
Corrigé de l'exercice 6
Q1: réponse c. (une asymptote horizontale)
Q2: réponse a. et réponse c. (une asymptote horizontale et une asymptote verticale ) |
![]() ;
; ![]() Réponse
Réponse ![]() et
et ![]()
![]() ;
; ![]() Réponse
Réponse ![]() et
et ![]()
![]() ;
; ![]() Réponse
Réponse ![]() et
et ![]()
![]() ;
; ![]() Réponse
Réponse ![]() et
et ![]()
![]() ;
; ![]() Réponse
Réponse ![]() et
et ![]()
![]() ;
; ![]() Réponse
Réponse ![]() et
et ![]()
![]() ;
; ![]() Réponse
Réponse ![]() et
et ![]()
![]() «
« ![]() ;
; ![]() Réponse
Réponse ![]()
![]() ;
; ![]() Réponse
Réponse ![]()
![]() ;
; ![]() Réponse
Réponse ![]()
![]() ;
; ![]() Réponse
Réponse ![]()
![]() ;
; ![]() Réponse
Réponse ![]()
![]() ;
; ![]() Réponse
Réponse ![]()
![]() ;
; ![]() Réponse
Réponse ![]()
![]() ;
; ![]() Réponse
Réponse ![]()
![]() :
:
![]() en
en ![]() , en
, en ![]() , en -5 à gauche et à droite.
, en -5 à gauche et à droite.![]() :
:
![]() ,
, ![]() tels que
tels que ![]() est définie sur
est définie sur ![]() , par
, par ![]() . Déterminer les valeurs de
. Déterminer les valeurs de ![]() ,
, ![]() en justifiant.
en justifiant.![]() définie sur
définie sur ![]() . Déterminer graphiquement les limites de
. Déterminer graphiquement les limites de ![]() en
en ![]() , en
, en ![]() , en -2 et en 2 à droite et à gauche. Indiquer les asymptotes.
, en -2 et en 2 à droite et à gauche. Indiquer les asymptotes.
![]() définie sur
définie sur ![]() donnée par
donnée par ![]() . La courbe
. La courbe ![]() admet comme asymptote la droite d’équation :
admet comme asymptote la droite d’équation :![]() b.
b. ![]() c.
c. ![]() d.
d. ![]()
![]() définie sur
définie sur ![]() par
par ![]() . La courbe
. La courbe ![]() admet commes asymptotes :
admet commes asymptotes :![]() b.
b. ![]() c.
c. ![]() d.
d. ![]()