Exercice 1
- Soit
 la fonction définie sur
la fonction définie sur ![Rendered by QuickLaTeX.com ]0;+\infty[](https://spe-maths.fr/wp-content/ql-cache/quicklatex.com-80243cc86f99e2d74411fff3ccaa6a1e_l3.png) par :
par : 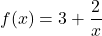 et
et 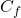 sa courbe représentative dans un repère orthonormé d’unité
sa courbe représentative dans un repère orthonormé d’unité 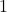 cm.
cm.
Calculer l’aire sous la courbe sur l’intervalle
sur l’intervalle ![Rendered by QuickLaTeX.com [1;4]](https://spe-maths.fr/wp-content/ql-cache/quicklatex.com-7d47d6bab2b045a261fb0309c3d5a687_l3.png) .
.
Ainsi l’aire sous la courbe
![Rendered by QuickLaTeX.com \mathscr{A}&=\displaystyle \int_1^4 f(x)dx \\&=\Big[3x+2\ln(x)\Big]_1^4 \\&=12+2\ln(4)-\left(3+2\ln(1)\right) \\&=12+2\ln(4)-3\\&=9+2\ln(4)\text{ u.a.}](https://spe-maths.fr/wp-content/ql-cache/quicklatex.com-0dd3a0f36c19ac286e662b04b10312f4_l3.png)
Or
Donc :
Exercice 2
Calculer
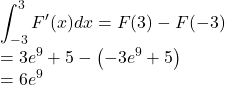
Exercice 3
![]()
![Rendered by QuickLaTeX.com m&=\dfrac{1}{1-(-2)}\displaystyle \int_{-2}^1 3x^2dx \\ &=\dfrac{1}{3}\Big[x^3\Big]_{-2}^1 \\ &=\dfrac{1^3-(-2)^3}{3} \\ &=\dfrac{1+8}{3} \\ &=3](https://spe-maths.fr/wp-content/ql-cache/quicklatex.com-19217812a0b3e56c9c84ef644e4c75fb_l3.png)
Exercice4
Calculer l’aire du domaine situé entre
![]() et
et ![]() sont deux fonctions continues sur
sont deux fonctions continues sur ![]() donc
donc ![]() et
et ![]() le sont aussi.
le sont aussi.
Il faut déterminer le signe de ![]() sur
sur ![]() .
.
Pour tout réel ![]() on a :
on a :
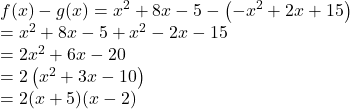
![]() est un polynôme du second degré dont le coefficient principal est
est un polynôme du second degré dont le coefficient principal est ![]() et les racines sont
et les racines sont ![]() et
et ![]() .
.
Or ![]() ,donc
,donc ![]() sur
sur ![]() .
.
Ainsi l’aire du domaine situé entre ![]() et
et ![]() sur
sur ![]() est :
est :
![Rendered by QuickLaTeX.com \mathscr{A}&=\displaystyle \int_{-4}^1 \left(g(x)-f(x)\right)dx \\ &=\int_{-4}^1\left(-2x^2-6x+20\right) dx \\ &=\left[-\dfrac{2}{3}x^3-3x^2+20x\right]_{-4}^1\\ &=-\dfrac{2}{3}-3+20-\left(\dfrac{128}{3}-48-80\right) \\ &=\dfrac{49}{3}+\dfrac{256}{3}\\ &=\dfrac{105}{3}](https://spe-maths.fr/wp-content/ql-cache/quicklatex.com-54d8c31ee60e69ba03eaabfca1108acf_l3.png)
Exercice 5
Exercice 6
![]()
- Montrer que la suite
 est croissante.
est croissante.
- On admet que pour tout réel
 de l’intervalle
de l’intervalle 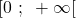 ,:
,: 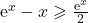 .
.
- Montrer que, pour tout entier naturel
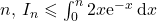 .
.
- Soit
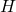 la fonction définie et dérivable sur l’intervalle
la fonction définie et dérivable sur l’intervalle 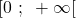 telle que :
telle que :
Déterminer la fonction dérivée![Rendered by QuickLaTeX.com \[H(x) = (- x - 1)\text{e}^{- x}\]](https://spe-maths.fr/wp-content/ql-cache/quicklatex.com-62c5a3be219ade20b381c73738e3ea81_l3.png)
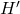 de la fonction
de la fonction 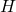 .
.
- En déduire que, pour tout entier naturel
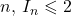 .
.
- Montrer que, pour tout entier naturel
- Montrer que la suite
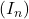 est convergente. On ne demande pas la valeur de sa limite.
est convergente. On ne demande pas la valeur de sa limite.
-
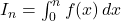 donc, pour tout
donc, pour tout  de
de  ,
,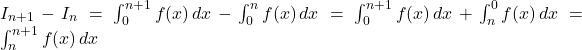
La fonction
 est positive sur
est positive sur 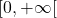 donc sur
donc sur 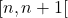 ; on peut en déduire que
; on peut en déduire que 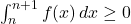 et donc que
et donc que 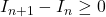 pour tout
pour tout 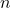 .
.La suite
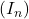 est donc croissante.
est donc croissante. -
-
Sur
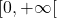 , on sait que
, on sait que 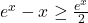 ; de plus, pour tout
; de plus, pour tout 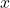 ,
, 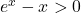 . Donc
. Donc 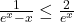 .
.On multiplie cette inégalité par
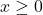 donc:
donc: 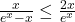 .
.D’après la croissance de l’intégration:
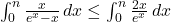 .
.Ce qui équivaut à
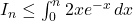 .
. -
La fonction
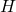 est dérivable sur
est dérivable sur 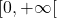 comme produit de fonctions dérivables et
comme produit de fonctions dérivables et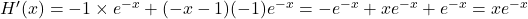 .
. -
On déduit de la question précédente que la fonction
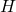 est une primitive de la fonction
est une primitive de la fonction 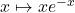 .
.Donc
![Rendered by QuickLaTeX.com \int_0^n x e^{-x} \, dx = [(-x-1)e^{-x}]_0^n = (-n-1)e^{-n} - [(-1)e^{0}] = 1 - (n+1)e^{-n}](https://spe-maths.fr/wp-content/ql-cache/quicklatex.com-487f4bb2f581a4ff2c96f8caf0fcd393_l3.png) .
.Pour tout
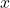 ,
, 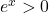 on a alors
on a alors 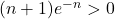 ce qui implique
ce qui implique 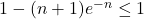 .
.Donc
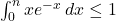 , en multipliant par 2 on obtient
, en multipliant par 2 on obtient 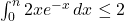 , finalement
, finalement 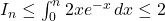 .
. -
La suite
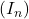 est croissante et majorée par 2 donc, d’après le théorème de la convergence monotone, la suite
est croissante et majorée par 2 donc, d’après le théorème de la convergence monotone, la suite 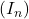 est convergente.
est convergente.
-