Vecteurs, droites et plans de l’espace
Vecteurs, droites et plans de l’espace
1-Produit scalaire
On appelle produit scalaire de deux vecteurs 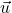 et
et 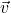 , le réel
, le réel 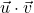 défini par :
défini par : 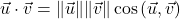 .
.
Dans le cas où l’espace est rapporté à un repère orthonormé 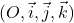 , le produit scalaire des vecteurs
, le produit scalaire des vecteurs 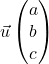 et
et 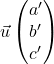 est donné par :
est donné par :
![Rendered by QuickLaTeX.com \[\vec{u} \cdot \vec{v}=aa'+bb'+cc'\]](https://spe-maths.fr/wp-content/ql-cache/quicklatex.com-85078f6c7af0ce2f9ce73f4fc17169f6_l3.png)
2-Représentation paramétrique d’une droite dans l’espace .
Soient  un point de l’espace et
un point de l’espace et 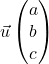 un vecteur non nul. La droite
un vecteur non nul. La droite  passant par A et de vecteur directeur
passant par A et de vecteur directeur 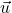 est l’ensemble des points de coordonnées
est l’ensemble des points de coordonnées 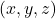 vérifiant le système paramétrique suivant :
vérifiant le système paramétrique suivant :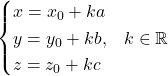
3-Equation cartésienne d’un plan dans l’espace .
On se place dans un repère orthonormée 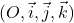 . Soit
. Soit 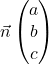 non nul.
non nul.
Une équation cartésienne d’un plan 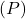 admettant
admettant 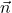 pour vecteur normal est :
pour vecteur normal est :
![Rendered by QuickLaTeX.com \[ax+by+cz+d=0, \text{ où d } \in \mathbb R\]](https://spe-maths.fr/wp-content/ql-cache/quicklatex.com-580de7ae240e0ea2e99737f6fe706d98_l3.png)
Réciproquement, Si un plan 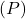 admet une équation cartésienne de la forme :
admet une équation cartésienne de la forme :
![Rendered by QuickLaTeX.com \[ax+by+cz+d=0\]](https://spe-maths.fr/wp-content/ql-cache/quicklatex.com-2928ea2011aac96cc4ecf223adc3c93b_l3.png)
alors le vecteur 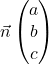 est normal à
est normal à 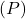 .
.
Exercices type Bac
1-Droites coplanaires, coordonnées du milieu, équation cartésienne d’un plan.
Exercice-1-geo-en
Exercice-1-geo-c
2-Equation cartésienne d’un plan, représentation paramétrique d’une droite.
Exercice-2-Geom-e
Exercice-2-geo-c
3-Equation cartésienne d’un plan, représentation paramétrique d’une droite, projeté orthogonale d’un point.
Exercice-3-geo-en
Exercice-3-geo-c
4-Equation cartésienne d’un plan, représentation paramétrique d’une droite.
Exercice-4-geo-en
Exercice-4-geo-c
5-Equation cartésienne d’un plan, représentation paramétrique d’une droite.
Exercice-5-geo-en
Exercice-5-geo-c
6-Equation cartésienne d’un plan, représentation paramétrique d’une droite.
Exercice-6-geo-en
Exercice-6-geo-c
7-Equation cartésienne d’un plan, représentation paramétrique d’une droite.
Exercice-7-geo-en
Exercice-7-geo-c
Télécharger l’énoncé et le corrigé de l’exercice 7
8- Intersection de deux plans, équation cartésienne d’un plan, équation paramétrique d’une droite, projeté orthogonal d’un point.
Exercice-8-Geom-e
Exercice-8-geom-c
Télécharger ici l’exercice 8
9- Équation cartésienne d’un plan, équation paramétrique d’une droite, mesure d’angle.
Exercice-geom-9-c
Indications pour l'exercice 9
- Montrer que les droites (LM) et (BD) sont \textcolor{red}{coplanaires} et sont contenues dans deux plans \textcolor{red}{strictement parallèles.}
- Déterminer les coordonnées des vecteurs $\overrightarrow{FL}$ et de $\overrightarrow{FE}$ puis utiliser l'égalité $\overrightarrow{FL}=\frac{2}{3}\overrightarrow{LE}$.
-
- La droite (BL) contient le point B et a pour vecteur directeur $\overrightarrow{BL}$.
- Déterminer une équation paramétrique de la droite (AE) qui passe par l’origine et a pour vecteur directeur $\vec{k}$, puis résoudre un système d'équations.
-
- Vérifier que $\vec{n}$ est orthogonal à 2 vecteurs non colinéaires du plan (BDL).
- Le plan (BDL) est l'ensemble des points P de coordonnées $(x,y,z)$ tels que $\overrightarrow{BP}\cdot \vec{n}=0$.
- Résoudre un système d'équations formé d'une équation paramétrique de la droite (EH) et d'une équation cartésienne du plan (BDL).
- Calculer les distances EL, EM, ES et utiliser la formules:
$\bullet $ Aire d'un triangle $\frac{base \times hauteur}{2}~~$ pour calculer l'aire de la base du tétraèdre.
$\bullet $ Volume d'un tétraèdre $\frac{aire ~de ~la~base \times hauteur}{3}~~$ .
On trouve EL=EM=2, Aire de la base =$2 m^2$ et Volume du tétraèdre $2m^3$
- Dans le triangle SLE rectangle en E utiliser $\tan \widehat{SLE}$.
On trouve $\widehat{SLE}=\approx{56,3}^{\circ}$ .
|
Exercice-geom-V1-C
Télécharger ici l’exercice 9
10- Coordonnées, longueurs, équation cartésienne d’un plan, équation paramétrique d’une droite.
Exercice-10-Geom-e
- AB = AD = 6.
- Le plan $\mathcal{P}$ a pour vecteur normal $\overrightarrow{\text{OH}}\left(0~;~2\sqrt{3}~;~\sqrt{6}\right)$ et passe par le point I$\left(\frac{3}{2}~;~\frac{3}{2}\sqrt{3}~;~0\right)$.
- Les coordonnées du point J$\left(\frac{3}{2}~;~\frac{1}{2}\sqrt{3}~;~\sqrt{6} \right)$ vérifient l'équation du plan $\mathcal{P}$.
$ \left\{\begin{array}{l c l}
x&=&3t - 3\\
y&=&t\sqrt{3}\\
z&=&2t\sqrt{6}
\end{array} \right.$ et K$\left(- \frac{3}{2}~;~\frac{\sqrt{3}}{2}~;~\sqrt{6} \right)$
- $\overrightarrow{\text{IJ}}\left(0~;~- \sqrt{3}~;~\sqrt{6} \right)$ et $\overrightarrow{\text{JK}}\left(- 3~;~0~;~0 \right)$.
Le produit scalaire : $\overrightarrow{\text{IJ}} \cdot \overrightarrow{\text{JK}}=0 $.
- On appelle L le milieu du segment [A,C] ,ses coordonnées sont $(-\frac{3}{2};\frac{3}{2}\sqrt{3};0)$. Vérifier que le point L appartient au plan $\mathcal{P}$, Ainsi L est l’intersection de la droite (AC) et le plan $\mathcal{P}$.
Le quadrilatère (IJKL) est un carré.
- Une équation paramétrique de la droite (BD) est :
$\left\{\begin{array}{l c l}
x&=&- 3t + 3\\
y&=&t\sqrt{3}\\
z&=&2t\sqrt{6}
\end{array} \right.$. On a donc :
$\overrightarrow{\text{O}M}\begin{pmatrix}- 3t + 3\\t\sqrt{3}\\2t\sqrt{6}\end{pmatrix}$ et $\overrightarrow{\text{I}M}\begin{pmatrix}- 3t + \frac{3}{2}\\t\sqrt{3} - \frac{3}{2}\sqrt{3}\\2t\sqrt{6}\end{pmatrix}$.
D'où on déduit : $\overrightarrow{\text{O}M} \cdot \overrightarrow{\text{I}M} = 36t^2 - 18t + \frac{9}{2}$.
Le triangle O$MI$ est rectangle en $M$ si $\overrightarrow{\text{O}M} \cdot \overrightarrow{\text{I}M}=0$ donc si $36t^2 - 18t + \frac{9}{2}=0$.
Or $\Delta = - 324 < 0$, donc le trinôme $~36t^2 - 18t + \frac{9}{2}~$ n'a pas de racines réelles : il n'existe pas de position du point $M$ tel que le triangle $OIM$ soit rectangle en $M$.
|
Corrigé
à venir
11- Baccalauréat spécialité maths 5 mai 2022 sujet 1.
Exercice 11
7points
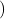
![]() et
et ![]() , le réel
, le réel ![]() défini par :
défini par : ![]() .
.![]() , le produit scalaire des vecteurs
, le produit scalaire des vecteurs ![]() et
et 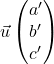 est donné par :
est donné par :![]()
![]() un point de l’espace et
un point de l’espace et ![]() un vecteur non nul. La droite
un vecteur non nul. La droite ![]() passant par A et de vecteur directeur
passant par A et de vecteur directeur ![]() est l’ensemble des points de coordonnées
est l’ensemble des points de coordonnées ![]() vérifiant le système paramétrique suivant :
vérifiant le système paramétrique suivant :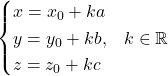
![]() . Soit
. Soit ![]() non nul.
non nul.![]() admettant
admettant ![]() pour vecteur normal est :
pour vecteur normal est :![]()
![]() admet une équation cartésienne de la forme :
admet une équation cartésienne de la forme :![]()
![]() est normal à
est normal à ![]() .
.