Rappel de cours sur les suites numériques
Si ![]() est une suite géométrique de raison
est une suite géométrique de raison ![]() avec
avec ![]() et de premier terme
et de premier terme ![]() On alors :
On alors :
![Rendered by QuickLaTeX.com \[u_n=u_0q^n \quad \text{et}\quad S_{n}=u_{0}+u_{1}+\ldots+u_{n}=\sum_{k=0}^{k=n}u_{k}=u_{0}\frac{1-q^{n+1}} {1-q}\]](https://spe-maths.fr/wp-content/ql-cache/quicklatex.com-3b94ed717a7bdcfa3aa72e8da75c9f16_l3.png)
Si ![]() est une suite géométrique de raison
est une suite géométrique de raison ![]() avec
avec ![]() et de premier terme
et de premier terme ![]() , où
, où ![]() . On alors
. On alors
![Rendered by QuickLaTeX.com \[u_n=u_ {n_0} q^{n- {n_0} } \quad \text{et}\quad S_{n}=u_{n_0}+u_{n_0+1}+\cdots+u_{n}=\sum_{k=n_0}^{k=n}u_{k}=u_{n_0}\frac{1-q^{n- {n_0} +1}} {1-q}\]](https://spe-maths.fr/wp-content/ql-cache/quicklatex.com-bd51ddc30ed7a70999615c63f9c8379e_l3.png)
![]()
![]()
![]() où
où ![]()
![]()
![]()
![]() où
où ![]()
Si ![]() alors
alors ![]()
Si ![]() alors
alors ![]()
Si ![]() alors la suite
alors la suite ![]() n’a pas de limite
n’a pas de limite
a) Théorème de comparaison : ![]() est
est ![]() sont deux suites telles qu’à partir d’un certain rang on a
sont deux suites telles qu’à partir d’un certain rang on a ![]() .
.
- si
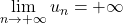 alors
alors 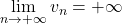
- si
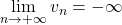 alors
alors 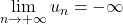
b) Théorème dit « des gendarmes » : Soit ![]() ,
, ![]() , et
, et ![]() trois suites réelles telles que
trois suites réelles telles que ![]() . Si à partir d’un certain rang,
. Si à partir d’un certain rang, ![]() alors
alors ![]() .
.
a) Définition 1 :
Une suite ![]() est dite:
est dite:
- minorée lorsque qu’il existe un réel
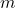 tel que, pour tout entier
tel que, pour tout entier 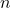 ,
, 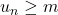 .
. - majorée lorsque qu’il existe un réel
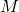 tel que, pour tout entier
tel que, pour tout entier 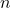 ,
, 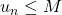
- bornée lorsqu’elle est à la fois minorée et majorée, c’est-à-dire lorsqu’il existe deux réels
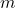 et
et 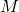 tels que, pour tout entier
tels que, pour tout entier 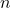 ,
, 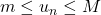 .
.
b) Définition 2 :
- Une suite est dite croissante si pour tout
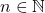 ,
, 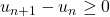 .
. - Une suite est dite décroissante si pour tout
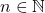 ,
, 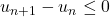
- Une suite est dite monotone si elle est croissante ou si elle est décroissante.
c) Convergence des suite monotone.
- Toute suite croissante et majorée converge.
- Toute suite décroissante et minorée converge.
- Toute suite croissante non majorée tend vers
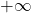 .
. - Toute suite décroissante non minorée tend vers

a) Définition
Une suite définie par récurrence est une suite définie par son premier terme et par une relation de récurrence, qui définit chaque terme à partir du précédent ou des précédents lorsqu’ils existent. Soit ![]() une fonction définie sur
une fonction définie sur ![]() et
et ![]() un nombre réel La suite
un nombre réel La suite ![]() définie par :
définie par :
![]() et pour tout entier naturel
et pour tout entier naturel ![]() ,
, ![]() est une suite récurrente.
est une suite récurrente.
b) Convergence d’une suite définie par récurrence
Soit ![]() une fonction définie sur
une fonction définie sur ![]() et
et ![]() un nombre réel.
un nombre réel.
Notons ![]() la suite définie par :
la suite définie par : ![]() et pour tout entier naturel
et pour tout entier naturel ![]() ,
, ![]() .
.
Si on démontre que la suite ![]() est convergente vers un nombre réel
est convergente vers un nombre réel ![]() et que la fonction
et que la fonction ![]() est continue en
est continue en ![]() , alors en passant à la limite dans la relation de récurrence, on obtient l’égalité
, alors en passant à la limite dans la relation de récurrence, on obtient l’égalité ![]() .
.
Ce qui veut dire que si une suite ![]() converge alors sa limite est solution de l’équation
converge alors sa limite est solution de l’équation ![]() .
.
a) Méthode
Soit ![]() une propriété relative à l’entier n et
une propriété relative à l’entier n et ![]() un entier.
un entier.
- Initialisation : On vérifie que la propriété
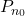 est vraie,
est vraie, - Hérédité : On montre que si la propriété
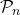 avec
avec  est vrais alors la propriété
est vrais alors la propriété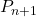 est aussi vraie.
est aussi vraie. - Conclusion : Pour tout entier naturel
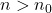 la propriété
la propriété 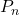 est vraie.
est vraie.
b) Remarques.
- La propriété
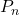 peut être de différentes natures égalité, inégalité, proposition . . .
peut être de différentes natures égalité, inégalité, proposition . . . - Les conditions initialisation et d’hérédité sont indispensables.
- La condition d’hérédité est une implication, on suppose que
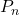 est vraie puis on montrer que
est vraie puis on montrer que 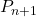 est vraie.
est vraie.
Exercices type bac
1-Suite récurrente, raisonnement par récurrence et limite et comparaison.
Télécharger ici l’exercice 1
2 Convergence monotone, théorème dit » des gendarmes », algorithme.
Télécharger ici l’exercice 2
3-Raisonnement par récurrence, suite géométrique, convergence monotone et limite.
Télécharger ici l’exercice 3
4-Suite géométrique, raisonnement par récurrence, sens de variation.
Télécharger ici l’exercice 4
5-Suite récurrente, Python, suite géométrique et limite.
Télécharger ici l’exercice 5
6-suite récurrente, Python, raisonnement par récurrence.
Télécharger l’exercice 6
7- Suite récurrente, tableur, suite géométrique.
Télécharger ici l’exercice 7
8-Suite récurrente, convergence monotone, Python.
Télécharger ici l’exercice 8
9-suite récurrente, suite géométrique axillaire , raisonnement par récurrence.Télécharger ici l’exercice 9
10 Suites récurrentes, suite géométrique, probabilités conditionnelles, limites.
Télécharger ici l’exercice 10
11- Exemple d’exercice sur 7 points.
-
-
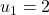 et
et 
- Pour tout
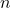 ,
, 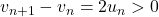 La suite
La suite -
Pour montrer l’hérédité :
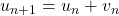 ; or
; or 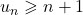 et
et 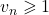 On en déduit que
On en déduit que - Pour tout
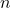 ,
, 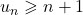 ; or
; or 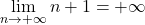 , donc par comparaison,
, donc par comparaison, 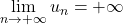
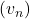 est strictement croissante, donc, pour tout
est strictement croissante, donc, pour tout 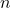 ,
, 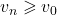 donc
donc 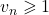
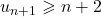
-
-
- Pour montrer l’hérédité :
![Rendered by QuickLaTeX.com \[2u_{n+1}^2-v_{n+1}^2=2(u_n+v_n)^2-(2u_n+v_n)^2=-2u_n^2+v_n^2=\]](https://spe-maths.fr/wp-content/ql-cache/quicklatex.com-9672c38dbaad99291f62b4e6bcc6dd01_l3.png)
![Rendered by QuickLaTeX.com \[=-(2u_n^2-v_n^2)=-(-1)^n=(-1)^{n+1}\]](https://spe-maths.fr/wp-content/ql-cache/quicklatex.com-892f06756faa2a38c7ea46212c948268_l3.png)
-
en déduit que :![Rendered by QuickLaTeX.com \[r_n^2-2=\left(\dfrac{v_n}{u_n}\right)^2-2=-\dfrac{2u_n^2-v_n^2}{u_n^2}=-\dfrac{(-1)^n}{u_n^2}=\dfrac{(-1)^{n+1}}{u_n^2}\]](https://spe-maths.fr/wp-content/ql-cache/quicklatex.com-bc8546e12ab5bc187eaf9a7dccf5064f_l3.png)
![Rendered by QuickLaTeX.com \[r_n^2 = 2 + \dfrac{(- 1)^{n+1}}{u_n^2}\]](https://spe-maths.fr/wp-content/ql-cache/quicklatex.com-bb4951f41305de1606d724a6357b56ac_l3.png)
- Pour montrer l’hérédité :
-
- On a pour tout
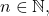
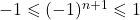 On divise par
On divise par -
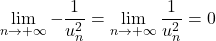 . Comme pour tout
. Comme pour tout 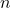 :
: 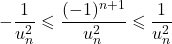 alors
alors 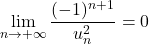 (Théorème des gendarmes)
(Théorème des gendarmes) -
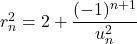 et
et 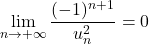 , donc:
, donc: 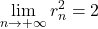 On peut en déduire que la suite
On peut en déduire que la suite - Pour tout entier naturel
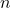 ,
,
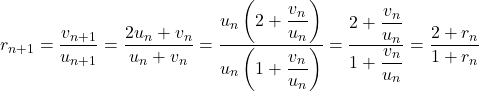
- La valeur renvoyée est la plus petite valeur de
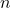 pour laquelle
pour laquelle 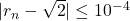 .
.
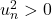 on obtient:
on obtient:
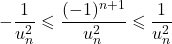
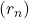 converge vers
converge vers 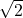
- On a pour tout
12- Baccalauréat spécialité maths 4 mai 2022 sujet 1.
13- Baccalauréat spécialité maths 5 mai 2022 sujet 2.