Rappel de cours
Soit ![]() et
et ![]() deux événements, avec
deux événements, avec ![]() . La probabilité conditionnelle de l’événement
. La probabilité conditionnelle de l’événement ![]() sachant
sachant ![]() , notée
, notée ![]() , est définie par
, est définie par
![]()

Règles d’utilisation d’un arbre pondéré
Règle 1 :La somme des probabilités issues d’un même nœud est égale à 1.  exemple:
exemple: 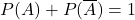 .
.
Règle 2 : Principe multiplicatif La probabilité d’un événement correspondant à un chemin est égale au produit des probabilités portées par les branches de ce chemin.  exemple :
exemple :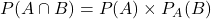 .
.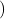
Règle 3 : La probabilité d’un événement est égale à la somme des probabilités des chemins qui aboutissent à sa réalisation. 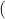 exemple :
exemple :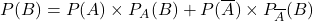 .
.
| Définition : On dit que deux événements ”Savoir que l’événement |
Remarque :
- Si
 et
et 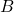 sont indépendants, on a aussi
sont indépendants, on a aussi 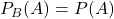 .
. - Ne pas confondre indépendance et incompatibilité
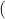
 et
et 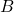 sont incompatibles, ou disjoints, lorsque
sont incompatibles, ou disjoints, lorsque 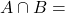 .
.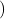
Propriété : Les événements ![]() et
et ![]() sont indépendants si et seulement si
sont indépendants si et seulement si ![]() .
.
a- Loi de Bernoulli
|
Définition : Une épreuve de Bernoulli est une expérience aléatoire qui ne comporte que deux issues, appelées généralement sucés S et échec E, de probabilités p et 1 − p.
|
|
Définition : Une variable aléatoire de Bernoulli est à valeur dans {0; 1} et associée à une épreuve de Bernoulli. La loi de probabilité est appelée loi de Bernoulli de paramètre p, |
Propriété : Si X suit une loi de Bernoulli de paramètre p, on a ![]() et
et ![]() , et donc
, et donc![]() .
.
b-Loi binomiale
|
Définition : On appelle schéma de Bernoulli la répétition d’épreuves de Bernoulli identiques et indépendantes |
|
Définition : Soit La variable aléatoire |
Exemple
Une urne contient 3 boules blanches et 2 boules noires. On tire 3 boules au hasard. Les 5 boules sont indiscernables au toucher et le tirage se fait avec remise. Les tirages sont identiques et indépendants. On a donc bien, dans ce cas, un schéma de Bernoulli.
On considère la variable aléatoire ![]() qui compte le nombre de boules blanches obtenues. La variable
qui compte le nombre de boules blanches obtenues. La variable ![]() suit une loi binomiale de paramètres n=3
suit une loi binomiale de paramètres n=3 ![]() nombre d’épreuves
nombre d’épreuves![]() et
et ![]()
![]() probabilité d’obtenir une boule blanche lors d’une épreuve
probabilité d’obtenir une boule blanche lors d’une épreuve![]() . On note
. On note ![]() .
.
Ce schéma peut être représenté par l’arbre suivant :

Grâce à l’arbre on voit que :
- Il y’a un seule chemin correspondant à 3 succès
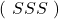 .
.
La probabilité d’avoir 3 succès ![]() c’est à dire 3 boules blanches
c’est à dire 3 boules blanches![]() est donc :
est donc :
![]()
- Il y a 3 chemins qui correspondent à 2 succès
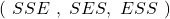 .
.
La probabilité d’obtenir 2 boules blanches est donc :
![]()
- Il y a également 3 chemins qui correspondent à un unique succès
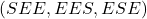 .
.
La probabilité d’obtenir une unique boule blanche est donc :
![]()
- Il y’a un seule chemin correspondant à 3 échecs
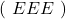 .
.
La probabilité de n’avoir aucune boule blanche est donc :
![]()
La loi de X est donc donnée par le tableau suivant :
![Rendered by QuickLaTeX.com \[\begin{array} {|r|r|}\hline x_i &0& 1 & 2 & 3 \\ \hline P(X=x_i)& \frac{27}{125} & \frac{54}{125} & \frac{36}{125} & \frac{8}{125} \\ \hline \end{array}\]](https://spe-maths.fr/wp-content/ql-cache/quicklatex.com-d80ec699d4694b2393331a70ff8f2e7b_l3.png)
On vérifie bien que : ![]()
c-Coefficients binomiaux
| Définition : On considère un arbre pondéré représentant une loi binomiale |
Exemple
On reprend le même exemple que précédemment. On a vu, par exemple, qu’il y avait 3 chemins correspondant à 2 succès. On a donc ![]() .
.
Il y’a un seule chemin correspondant à 3 succès. On a donc ![]() .
.
Les deux autres coéfficient binomiaux sont : ![]() et
et ![]() .
.
Pour calculer un coefficient binomial à l’aide d’une calculatrice on utilise la commande nCr.
|
Théorème : Soit X une variable aléatoire de loi
|
On lance 7 fois une pièce équilibrée et on appelle X la variable aléatoire qui compte le nombre de fois où l’on obtient face.
X suit une loi binomiale de paramètres n=7 et ![]() .
.
La probabilité d’obtenir 3 fois face est :
![]()
À l’aide d’une calculatrice on calcule le coefficient binomial ![]() =35.
=35.
Donc : ![]()
Exercices type BAC
1) arbre pondéré, probabilité conditionnelle, loi binomiale.
Télécharger ici l’exercice 1
2)Loi binomiale, probabilité conditionnelle, arbre pondéré.
Télécharger ici l’exercice 2
3
Télécharger ici l’exercice 3
4 Combinaison, variable aléatoire, loi binomiale
Télécharger ici l’exercice 4
5 Arbre de probabilités, loi binomiale
Télécharger ici l’exercice 5
6 Arbre de probabilités, variable aléatoire, loi binomiale
Télécharger ici l’exercice 6
7 Arbre de probabilités, loi binomiale
8 Arbre de probabilité, suite géométrique auxiliaire, raisonnement par récurrence, limite d’une suite.
9 Arbre de probabilité, loi binomiale, Python
Indications pour l'exercice 9.
|
11 Arbre de probabilité, python, loi binomiale.

![Rendered by QuickLaTeX.com \[\begin{array} {|r|r|}\hline x_i & 0 & 1 \\ \hline P(X=x_i)& 1-p &p \\ \hline \end{array}\]](https://spe-maths.fr/wp-content/ql-cache/quicklatex.com-ced55254a14559ef4d95fa5384a80b62_l3.png)