| Primitive d’une fonction: Une fonction |
|
Exemples
|
Si l’ensemble des primitives de |
|
Propriété :
|
Primitives des fonctions de référence.
Primitives des fonctions de la forme ![]() .
.
1- Montrer qu’une fonction est une primitive.
Télécharger ici l’énoncé et le corrigé de l’exercice 1
2- ![]() primitive ,
primitive , ![]() primitives et
primitives et ![]() primitive d’une fonction.
primitive d’une fonction.
Télécharger ici l’énoncé et le corrigé de l’exercice 2
Équations différentielles
Equation différentielle 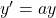
Soit ![]() un réel fixé
un réel fixé
L’équation différentielle ![]() sur ℝ admet pour solutions les fonctions
sur ℝ admet pour solutions les fonctions ![]() définies par :
définies par : ![]() (où
(où ![]() est une constante réelle), et ce sont les seules solutions.
est une constante réelle), et ce sont les seules solutions.
Exemple
Les solutions de l’équation différentielle ![]() sur
sur ![]() sont les fonctions
sont les fonctions ![]() définies par :
définies par : ![]() (où
(où ![]() est une constante réelle).
est une constante réelle).
Equation différentielle 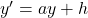
Soit ![]() un réel fixé et
un réel fixé et ![]() une fonction donnée.
une fonction donnée.
Les solutions de l’équation différentielle ![]() sur
sur ![]() s’obtiennent en déterminant une solution particulière de cette équation, et en lui ajoutant les solutions de l’équation différentielle
s’obtiennent en déterminant une solution particulière de cette équation, et en lui ajoutant les solutions de l’équation différentielle ![]() .
.
Exemple
On considère l’équation différentielle (E): ![]() sur
sur ![]() .
.
-
Déterminer le réel
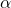 pour que la fonction
pour que la fonction 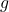 définie sur
définie sur 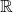 par
par 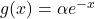 soit une solution particulière de l’équation (E).
soit une solution particulière de l’équation (E).
- Montrer que
 est solution de (E) équivaut à
est solution de (E) équivaut à  solution de (E’):
solution de (E’): 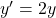 .
.
- En déduire les solutions de (E).
Solution
-
On a:
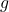 est solution de (E) si et seulement si
est solution de (E) si et seulement si 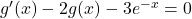 soit
soit 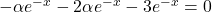
On factorise par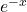 on obtient
on obtient 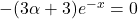 comme
comme 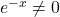 alors
alors 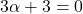 donc
donc 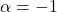 .
Donc
.
Donc 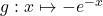 est une solution particulière de l’équation (E).
est une solution particulière de l’équation (E).
 est solution de (E) si et seulement si
est solution de (E) si et seulement si 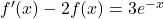
si et seulement si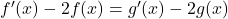
si et seulement si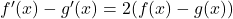
si et seulement si solution de (E’):
solution de (E’): 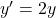 .
.
- Or les solutions de
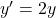 sont les fonctions
sont les fonctions 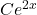 (où C est un réel quelconque).
(où C est un réel quelconque).
Par conséquent: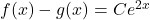 (où C est un réel quelconque)
(où C est un réel quelconque)
Et par là: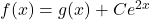
Donc les fonctions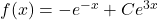 (où C est un réel quelconque) sont les solutions de (E).
(où C est un réel quelconque) sont les solutions de (E).
Equation différentielle 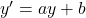
Où ![]() et
et ![]() sont des réels fixés.
sont des réels fixés.
L’équation différentielle ![]() sur
sur ![]() admet pour solution les fonctions
admet pour solution les fonctions ![]() définies par
définies par ![]() .
.
Exercice 3
On considère l’équation différentielle (E): ![]() sur
sur ![]() .
.
-
Proposer une fonction
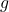 définie sur
définie sur 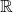 qui est solution de l’équation (E).
qui est solution de l’équation (E).
- Montrer que
 est solution de l’équation (E) si et seulement si
est solution de l’équation (E) si et seulement si  est solution de l’équation (E’):
est solution de l’équation (E’): 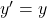 .
.
- En déduire les solutions de l’équation (E).
- On note que (E) l’équation différentielle:
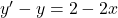
La fonction définie sur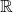 par
par 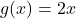 est solution de (E).
est solution de (E).
En effet :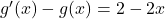
 est solution de (E) si et seulement si
est solution de (E) si et seulement si 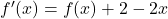
si et seulement si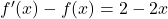
si et seulement si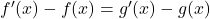
si et seulement si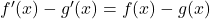
si et seulement si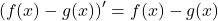
si et seulement si solution de (E’):
solution de (E’): 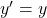 .
.
- Or les solutions de
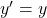 sont les fonctions
sont les fonctions 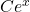
 où
où  est une constante réelle quelconque
est une constante réelle quelconque  .
.
Par conséquent: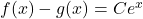
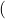 avec
avec 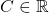
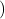
Par suite :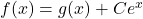
Donc les fonctions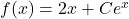
 avec
avec 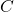 est une constante réelle quelconque) sont les solutions de (E).
est une constante réelle quelconque) sont les solutions de (E).
Exercice 4
1-
a)Résoudre l’équation
b) Déterminer la fonction solution qui vérifie de plus
2- Soit
a) Résoudre
b) Déterminer la solution de
a) D’après le cours l’équation différentielle
b)
2-
a) l’équation différentielle s’écrit
b)
Exercice 5  Amérique du Sud novembre 2008
Amérique du Sud novembre 2008 
- Résoudre l’équation différentielle :
dont l’inconnue est une fonction définie et dérivable sur![Rendered by QuickLaTeX.com \[2y' + y = 0 \quad (\text{E}),\]](https://spe-maths.fr/wp-content/ql-cache/quicklatex.com-23b7b161ffecd52412c6de8defc0f594_l3.png)
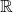 .
On considère l’équation différentielle :
.
On considère l’équation différentielle :
- Déterminer deux réels
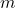 et
et 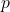 tels que la fonction
tels que la fonction  définie sur
définie sur 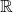 par :
par :
![Rendered by QuickLaTeX.com \[f(x) = \text{e}^{- \frac{x}{2}}\left(mx^2 + px\right)~ \text{soit solution de (E}').\]](https://spe-maths.fr/wp-content/ql-cache/quicklatex.com-5d7f04ab68ee50051902d20e5102b634_l3.png)
- Soit
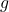 une fonction définie et dérivable sur
une fonction définie et dérivable sur 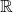 .
Montrer que
.
Montrer que 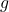 est solution de l’équation (E
est solution de l’équation (E ) si et seulement si
) si et seulement si  est solution de l’équation (E).
Résoudre l’équation (E
est solution de l’équation (E).
Résoudre l’équation (E ).
).
![]()
- D’après le cours cette équation a pour solutions les fonctions :
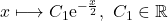 .
. -
![Rendered by QuickLaTeX.com \[2y' + y = \text{e}^{- \frac{x}{2}}(x + 1) \quad (\text{E}')\]](https://spe-maths.fr/wp-content/ql-cache/quicklatex.com-c385dff04e6b884d841cd29c4bd5c47d_l3.png)
-
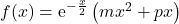 :
:  est un produit de fonctions dérivables sur
est un produit de fonctions dérivables sur 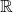 , elle est donc dérivable sur
, elle est donc dérivable sur 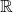 et
et
![Rendered by QuickLaTeX.com \[f'(x) = - \dfrac{1}{2}\text{e}^{- \frac{x}{2}}\left(mx^2 + px\right) + (2mx + p)\text{e}^{- \frac{x}{2}}\]](https://spe-maths.fr/wp-content/ql-cache/quicklatex.com-d315f9f3d2040b9b5a02c3e861d258d8_l3.png)
 est solution de E
est solution de E si et seulement si
si et seulement si 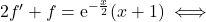
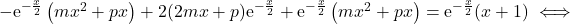
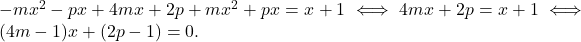 Cette fonction affine est nulle si et seulement si
Cette fonction affine est nulle si et seulement si 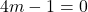 et
et 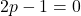 , soit si
, soit si 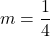 et
et 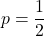 .
.
-
On a :
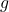 et
et  solutions de E
solutions de E si et seulement si
si et seulement si
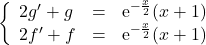 par différence des 2 équations du système on obtient :
par différence des 2 équations du système on obtient :
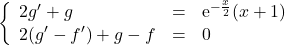 Donc
Donc 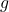 est solution de l’équation (E
est solution de l’équation (E ) si et seulement si
) si et seulement si  est solution de l’équation (E)
%Résoudre l’équation (E
est solution de l’équation (E)
%Résoudre l’équation (E ).
On a donc
).
On a donc  d’où
d’où 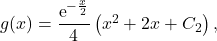
-