Application de la continuité
Exercice 1
On considère la fonction  définie sur
définie sur 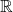 par
par
![Rendered by QuickLaTeX.com \[f(x) = \begin{cases} -2x + 3 & \text{si } x \leq 2 \\ m x - 3 & \text{si } x > 2 \end{cases}\]](https://spe-maths.fr/wp-content/ql-cache/quicklatex.com-dad3f3cef7e9c973b86b29f180c5551a_l3.png)
Déterminer la valeur de 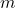 pour laquelle la fonction
pour laquelle la fonction  est continue sur
est continue sur 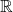 , puis réaliser une représentation graphique.
, puis réaliser une représentation graphique.
La fonction  est continue en tout point
est continue en tout point 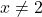 car elle est affine sur
car elle est affine sur ![Rendered by QuickLaTeX.com ]-\infty, 2[](https://spe-maths.fr/wp-content/ql-cache/quicklatex.com-e84bd1b05be2e5aead047037eb5f40f5_l3.png) et sur
et sur ![Rendered by QuickLaTeX.com ]2,-\infty[](https://spe-maths.fr/wp-content/ql-cache/quicklatex.com-efab85f25ba46a14237f932503f92968_l3.png) . Pour
. Pour 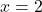 on a
on a 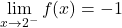 et
et  et
et 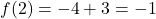 . La fonction
. La fonction  est continue en
est continue en 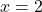 si et seulement si les limites à gauche et à droite de 2 sont égales à
si et seulement si les limites à gauche et à droite de 2 sont égales à 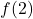 , Autrement dit
, Autrement dit 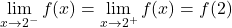 ce qui équivalent à
ce qui équivalent à 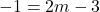 donc
donc 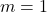 . Par conséquent la fonction
. Par conséquent la fonction 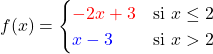 est continue sur
est continue sur 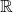 .
.
représentation graphique.
Exercice 2
Soit une fonction  dont le tableau de variation est
dont le tableau de variation est
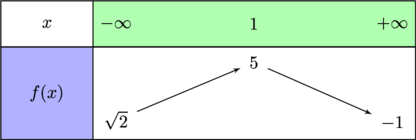
Déterminer le nombre de solution de l’équation 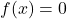 sur
sur 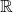 .
.
D’après le tableau de variation;
- Sur l’intervalle
![Rendered by QuickLaTeX.com ]-\infty,1]](https://spe-maths.fr/wp-content/ql-cache/quicklatex.com-b7faa72af56efbfd258a467731c8c06d_l3.png) on a
on a ![Rendered by QuickLaTeX.com f(x) \in ]\sqrt{2},5]](https://spe-maths.fr/wp-content/ql-cache/quicklatex.com-142a163059cce75a2a866b50c32dfaf3_l3.png) donc l’équation ne possède pas de solution car 0 …….
donc l’équation ne possède pas de solution car 0 …….
- Sur l’intervalle
![Rendered by QuickLaTeX.com ]1,+\infty[](https://spe-maths.fr/wp-content/ql-cache/quicklatex.com-ae35f60d6953fc13977e40d4675e7503_l3.png) , la fonction
, la fonction  est continue et strictement décroissante.
est continue et strictement décroissante. 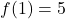 ,
, 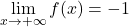 et
et 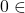 ]-1,5[ donc d’après le corollaire du TVI l’équation
]-1,5[ donc d’après le corollaire du TVI l’équation 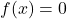 possède une solution unique sur
possède une solution unique sur ![Rendered by QuickLaTeX.com ]1,+\infty[](https://spe-maths.fr/wp-content/ql-cache/quicklatex.com-ae35f60d6953fc13977e40d4675e7503_l3.png) .
.
Par conséquent, l’équation 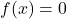 possède exactement une seule solution sur
possède exactement une seule solution sur 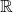 .
.
Exercice 3
Soit $f$ la fonction définie sur $[1 ; 2]$ par $f(x)=x^{3}+x+5$.
Montrer que l'équation $f(x)=10$ admet une solution unique $\alpha$ sur $[1 ; 2]$, puis déterminer un encadrement de $\alpha$ d'amplitude 0,1 .
|
$f^{\prime}(x)=3 x^{2}+1 .$ Comme $x^{2} \geq 0$ alors $3 x^{2}+1 > 0$, $f'$ est strictement positif.
La fonction $f$ est continue et strictement croissante sur $[1 ; 2]$.
Or 10 est un nombre compris entre $f(1)=7$ et $f(2)=15$,
Donc, d'après le corollaire du théorème des valeurs intermédiaires, l'équation $f(x)=10$
admet une unique solution a sur $[1 ; 2]$.
On déterme un encadrement de $\alpha$ par essais successifs à l'aide de la calculatrice avec un pas de $0.1$ entre $1$ et $2$.
\begin{array}{|c|c|c|c|c|c|c|}
\hline x & 1 & ... & 1,5 & 1,6 & 1,7 & ... & 2\\
\hline f(x) &7 & ... & 9,88 & 10,70 & 11,61& ... & 15\\
\hline
\end{array}
Les valeurs de $f(x)$ sont arrondies à $10^{-2}$ près.
comme $f(\alpha)=10 \in [f(1.5),f(1.6)]$ alors $1,5 < \alpha <1,6$
L'encadrement cherché est: $1,5 < \alpha <1,6$. Et puisque $1,6-1,5=0,1$, l'amplitude est bien égale à 0,1 .
|
Exercice 4
- Démontrer que l'équation $2x^3−6x=6$ admet au moins une solution dans $\mathbb R$.
- Démontrer que l'équation $2x^3−6x=6$ admet exactement une solution $\alpha$ dans $\mathbb R$.
- Donner une valeur approchée de α à $10^{-2}$ près.
- Discuter, suivant les valeurs du réel $k$, le nombre de solution(s) de l'équation $2x^3−6x=k$.
|
- Posons $f(x)=2x^3−6x$. La fonction $f $ est définie sur $\mathbb R$. La figure suivante illustre la représentation graphique de $f$.

$f$ étant un polynôme elle est continue sur $\mathbb R$.
On a $f(2)=4$ et $f(3)=36$. Comme $6 \in [4,36]$ d'après le TVI, l'équation $f(x)=6$ admet au moins une solution dans $\mathbb R$.
- $f$ étant un polynome, $f$ est dérivable sur $\mathbb R$. Pour tout réel $x$, $f'(x)=6(x^2-1)$.
$f'(x) \geq 0$ pour $x \in ]-\infty,-1] \cup [1, +\infty[$ et $f'(x) < 0$ pour $x \in ]-1,1[$. On a $\lim\limits_{x \to -\infty}f(x)=-\infty$
et $\lim\limits_{x \to +\infty}f(x)=+\infty$, $f(-1)=4$ et $ f(1)=-4$ d'où le tableau de variation de $f$:

D'après le tableau de variation de $f$, l'équation $f(x)=6$ n'admet pas de solution dans l'intervalle $]-\infty,1]$ car $ \forall x \in ]-\infty,1], ~f(x) \leq 4$ et puisque $6 \in ]-4,+\infty[$ l'équation $f(x)=6$ admet exactement une solution dans l'intervalle $ [1,+\infty[$.
- D'après la représentation graphique de $f$,la solution $\alpha$ de l'equation $f(x)=6$ est proche de 2. Avec la calculatrice, on réalise un tableau de valeurs de $f$ en commençant par $x=2$ à $x=2,2$ par pas de 0,01. Voici une partie de ce tableau.
\begin{array} {|r|r|}\hline x & .... & 2,1 & 2,11 & 2,12 & ...\\ \hline f(x) & .... & 5,922 & 6,12786 & 6,336256 & .....\\ \hline \end{array}
On remarque que $2,1< \alpha < 2,11$. Pour plus de précision on refait un tableau de valeurs en commençant par $x=2$ avec un pas plus petit soit $0,001$.
\begin{array} {|r|r|}\hline x & 2,1 & 2,101 & 2,102 & 2,103 & 2,104 \\ \hline f(x) & 5,922 & 5,942472602 & 5,962970416 & 5,983493454 & 6,004041728 \\ \hline \end{array}
On voit que $2,103< \alpha < 2,104$. Donc $\alpha \approx{2,10}$ à $10^{-2} $ près.
D'après le tableau de variation de la fonction $f$ :

- si $k > 4$ l'équation $3x^3-6x=k$ admet une seul solution.
- Si $-4 < k < 4$ l'équation $3x^3-6x=k$ admet trois solutions
- Si $k=-4$ ou $ k= 4$ l'équation $3x^3-6x=k$ admet deux solutions.
|
Exercice 5

est la fonction définie sur
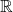
par :
![Rendered by QuickLaTeX.com \[ f(x) = x^3 - 3x - 4. \]](https://spe-maths.fr/wp-content/ql-cache/quicklatex.com-d16a285b1d800ead7389fc4149f2171e_l3.png)
-
- Justifier que
 est continue sur
est continue sur 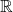 .
.
- Étudier les limites de
 en
en  et en
et en  .
.
- Étudier les variations de
 . Dresser son tableau de variation.
. Dresser son tableau de variation.
-
- Vérifier qu’il existe un réel
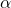 unique tel que
unique tel que 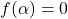 .
.
- Donner un encadrement de
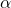 d’amplitude
d’amplitude 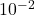 .
.
- Étudier le signe de la fonction
 .
.
$f$ est la fonction définie sur $\mathbb{R}$ par :
\[ f(x) = x^3 - 3x - 4. \]
- $f$ est continue sur $\mathbb{R}$ car c'est une fonction polynôme.
- Pour tout $x \in \mathbb{R}$, $f(x) = x^3 - 3x - 4 = x^3\left(1-\dfrac{3}{x^2}-\dfrac{4}{x^3}\right)$.
$\lim\limits_{x\rightarrow -\infty}\left(1-\dfrac{3}{x^2}-\dfrac{4}{x^3}\right)=1$ et $\lim\limits_{x\rightarrow -\infty}x^3=-\infty$ donc $\lim\limits_{x\rightarrow -\infty}f(x)=-\infty$ (par produit)
De même, $\lim\limits_{x\rightarrow +\infty}f(x)=+\infty$.
- $f$ est dérivable sur $\mathbb{R}$ comme une fonction polynôme.
\[f'(x) = 3x^2 - 3 = 3\left(x^2-1\right)=3(x+1)(x-1).\]
$f'(x) = 0$ pour $x=-1$ ou $x=1$.
$f'(x)$ est un polynôme du second degré ; $f'(x)$ est positif, en dehors des racines, donc sur $]-\infty~;~-1]\cup[1~;~+\infty[$ et négatif sur $[-1~;~1]$.
$f(-1)=-2$ et $f(1)=-6$

- D'après le tableau de variation, $f(x) \leqslant -2$ et sur $]-\infty~;~1[$.
Sur $]1~;~+\infty[$, $f$ est continue, $f(1) < 0$ et $\lim\limits_{x\rightarrow +\infty}f(x)=+\infty$.
D'après le théorème des valeurs intermédiaires, l'équation $f(x)=0$ admet une solution, unique puisque $f$ est strictement croissante sur cet intervalle. On la note $\alpha$.
- À l'aide de la calculatrice, on trouve $2,19<\alpha<2,20$.
- On en déduit le signe de $f(x)$ :
$f(x) < 0$ pour $x \in ]-\infty, \alpha[$ et $f(x) \geq 0$ pour $x \in [\alpha, +\infty[$
|
![]() définie sur
définie sur ![]() par
par![Rendered by QuickLaTeX.com \[f(x) = \begin{cases} -2x + 3 & \text{si } x \leq 2 \\ m x - 3 & \text{si } x > 2 \end{cases}\]](https://spe-maths.fr/wp-content/ql-cache/quicklatex.com-dad3f3cef7e9c973b86b29f180c5551a_l3.png)
![]() pour laquelle la fonction
pour laquelle la fonction ![]() est continue sur
est continue sur ![]() , puis réaliser une représentation graphique.
, puis réaliser une représentation graphique.![]() est continue en tout point
est continue en tout point ![]() car elle est affine sur
car elle est affine sur ![]() et sur
et sur ![]() . Pour
. Pour ![]() on a
on a ![]() et
et ![]() et
et ![]() . La fonction
. La fonction ![]() est continue en
est continue en ![]() si et seulement si les limites à gauche et à droite de 2 sont égales à
si et seulement si les limites à gauche et à droite de 2 sont égales à ![]() , Autrement dit
, Autrement dit ![]() ce qui équivalent à
ce qui équivalent à ![]() donc
donc ![]() . Par conséquent la fonction
. Par conséquent la fonction 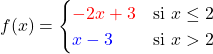 est continue sur
est continue sur ![]() .
.
![]() dont le tableau de variation est
dont le tableau de variation est
![]() sur
sur ![]() .
.![Rendered by QuickLaTeX.com ]-\infty,1]](https://spe-maths.fr/wp-content/ql-cache/quicklatex.com-b7faa72af56efbfd258a467731c8c06d_l3.png) on a
on a ![Rendered by QuickLaTeX.com f(x) \in ]\sqrt{2},5]](https://spe-maths.fr/wp-content/ql-cache/quicklatex.com-142a163059cce75a2a866b50c32dfaf3_l3.png) donc l’équation ne possède pas de solution car 0 …….
donc l’équation ne possède pas de solution car 0 …….
![Rendered by QuickLaTeX.com ]1,+\infty[](https://spe-maths.fr/wp-content/ql-cache/quicklatex.com-ae35f60d6953fc13977e40d4675e7503_l3.png) , la fonction
, la fonction  est continue et strictement décroissante.
est continue et strictement décroissante. 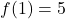 ,
, 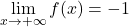 et
et 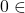 ]-1,5[ donc d’après le corollaire du TVI l’équation
]-1,5[ donc d’après le corollaire du TVI l’équation 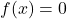 possède une solution unique sur
possède une solution unique sur ![Rendered by QuickLaTeX.com ]1,+\infty[](https://spe-maths.fr/wp-content/ql-cache/quicklatex.com-ae35f60d6953fc13977e40d4675e7503_l3.png) .
.![]() possède exactement une seule solution sur
possède exactement une seule solution sur ![]() .
.![]()
 est continue sur
est continue sur 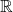 .
. en
en  et en
et en 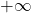 .
. . Dresser son tableau de variation.
. Dresser son tableau de variation.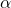 unique tel que
unique tel que 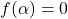 .
.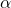 d’amplitude
d’amplitude 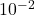 .
. .
.
