Programmer en Python en spécialité maths

Aide mémoire des instructions de bases de Python
| Saisie d'une variable |
|
| Affichage | print X affiche le contenu de la variable X print "Ceci est une chaîne de caractère" affiche un texte print "la valeur de X est ",X affiche texte et variable : |
| Affectation | Y=X affecte la valeur de X à la variable Y |
| Commentaires | Une ligne de commentaire doit être précédée par le signe # |
| Boucle for | for i in range(n) : $\qquad $ bloc d'instructions La variable i parcourt tous les entiers de 0 à n-1 le bloc d'instructions est donc répétée n fois Le décalage vers la droite $($ indentation $)$ indique que les instructions font partie de la boucle for. |
| Boucle while (Tant que) | while condition : $\qquad $ bloc d'instructions Le décalage vers la droite $($ indentation $)$ indique que les instructions font partie de la boucle while. |
| Fonctions | Def calcul(x,y, z,$\cdots$ ): $\qquad $ instructions $\cdots$ s=$\cdots$ $\qquad $ return(s) $\\$ x,y,z,$\cdots$ sont les arguments de la fonction calcul. On peut aussi retourner plusieurs valeurs : return(s,r,u,$\cdots$ ). Respecter l'indentation. |
| Test | X==Y $($ égal $)$ X!=Y $($ différent $)$ X>Y $($ strictement supérieur $)$ X < Y $($ strictement inférieur $)$ X>=Y $($ supérieur ou égal $)$ X<=Y $($ inférieur ou égal $)$ |
| Si | if condition 1 : $\qquad $ bloc d'instruction 1 elif condition 2 : $\qquad $ bloc d' instruction 2 else : $\qquad $bloc d' instruction 3 Le décalage vers la droite indique que les instructions font partie de la structure conditionnelle. |
| Opérations élémentaires | addition + soustraction - multiplication * puissance ** division / reste de division entière % exemple 5%2 donne 1 quotient de division entière // Exemple 5//2 donne 2 |
| Utiliser les fonctions mathématiques. | from math import * à mettre au début du programme pour importer le module math qui contient les définitions de nombreuses fonctions mathématiques telles que sqrt ,exp ,sin, cos , tan , pi ... Exemple de site qui donne des fonctions pythons |
Suites avec Python
Exercice1
On place un capital de 1000€ sur un compte rémunéré à 4% par an.
Ecrire un programme Python qui calcule le nombre d’années au bout
desquelles le capital sera doublé.
Le capital doublera au bout de 18 ans.
Exercice 2
Soit ![]() la suite définie pour tout
la suite définie pour tout ![]() ,
, ![]() .
.
Ecrire un programme langage Python permettant de calculer pour un ![]() donné la valeur de
donné la valeur de ![]() . Afficher les termes
. Afficher les termes ![]() à
à ![]()
Vous pouvez modifier le programme et l’exécuter en cliquant sur run. Vous pouvez afficher uniquement les termes avec print(u(k)).
Exercice 3
Ecrire un programme Python qui calcule les termes de la suite ![]() définie par l’expression
définie par l’expression
![]() . Afficher en particulier les termes
. Afficher en particulier les termes ![]() et
et ![]()
Qu’observe-t-on pour des valeurs de plus en plus grandes de n ?
On remarque que pour des valeurs de plus en plus grandes de n, les termes de la suite ![]() se rapprochent de 5.
se rapprochent de 5.
Exercice 4
Soit ![]() la suite définie par
la suite définie par ![]() et pour tout
et pour tout ![]() ,
, ![]() .
.
On admet que la suite ![]() est positive et croissante voir
est positive et croissante voir ![]() exercice 6
exercice 6 ![]()
Ecrire un programme langage Python qui donne la plus petite valeur de ![]() à partir de laquelle
à partir de laquelle ![]() dépasse 12000.
dépasse 12000.
Le programme affiche la valeur de n=41. Vous pouvez modifier le programme pour afficher la valeur de ![]() correspondante en utilisant print(n,u(n) ) à l’extérieur de la boucle while ou bien afficher toutes les valeurs de
correspondante en utilisant print(n,u(n) ) à l’extérieur de la boucle while ou bien afficher toutes les valeurs de ![]() avec print(n,u(n) ) à l’interieur de la boucle.
avec print(n,u(n) ) à l’interieur de la boucle.
Exercice 5
On considère la suite ![]() définie par
définie par ![]() et pour tout entier naturel
et pour tout entier naturel ![]() par
par ![]() .
.
On admet que cette suite est positive et tend vers 0. Ecrire un programme Python qui affiche la plus petite valeur de ![]() pour laquelle
pour laquelle ![]() .
.
Les termes de la suites sont positifs, le programme commence le calcule de ces termes par u=1, et continue tant que ![]() et s’arrête lorsque le terme u devient inférieur ou égal à 0,001 et renvoie le rang N correspondant.
et s’arrête lorsque le terme u devient inférieur ou égal à 0,001 et renvoie le rang N correspondant.
Afficher les termes de la suite avec l’instruction :
print " n =",n,"u=",u
à l’intérieur de la boucle while pour voir que u diminue jusqu’à devenir ![]() .
.
Exercice 6
On considère la suite définie par : pour tout entier naturel ![]() ,
, ![]() .
.
- Exprimer
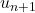 en fonction de
en fonction de 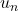 pour tout naturel
pour tout naturel  .
. - Donner le sens de variation de
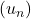 ainsi que sa limite.
ainsi que sa limite. - Ecrire un programme en Python permettant de déterminer la plus petite valeur
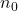 telle que
telle que 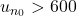 . Afficher la valeur de
. Afficher la valeur de 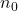
- Pour tout naturel
 :
: 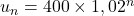 .
.
On reconnaît ici la formule explicite donnant le terme de rang d’une suite géométrique de raison 1,02 de premier terme
d’une suite géométrique de raison 1,02 de premier terme 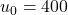 . Par conséquent, on a la formule de récurence suivante : pour tout naturel
. Par conséquent, on a la formule de récurence suivante : pour tout naturel  :
: 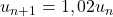 .
. - Comme
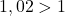 , alors la suite
, alors la suite 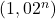 est strictement croissante. Et comme
est strictement croissante. Et comme 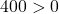 , la suite
, la suite 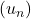 est également strictement croissante. Par ailleurs: Comme
est également strictement croissante. Par ailleurs: Comme 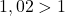 , on a:
, on a: 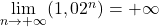 Or
Or 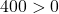 . Donc
. Donc 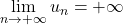
- Deux algorithmes possibles :
- Un premier algorithme qui utilise la formule de récurrence, la variable N contient la valeur
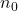 cherchée :
cherchée :
- Un deuxième algorithme qui utilise la formule explicite :
Exercice 7  12 minutes
12 minutes  1,2 points
1,2 points
On considère la suite ![]() u_n
u_n ![]() définie par
définie par ![]() et
et ![]() .
.
Recopier le script python ci-dessous et compléter les lignes 3 et 6 pour que liste(k) prenne en paramètre un entier naturel k et renvoie la liste des premières valeurs de la suite ![]() u_n
u_n ![]() de
de ![]() à
à ![]() .
.

Avec l’istruction print liste(5) afficher une liste de 6 premiers termes de la suite ![]() . Vérifier que les termes de
. Vérifier que les termes de ![]() sont les inverses des entiers naturels non nuls.
sont les inverses des entiers naturels non nuls.
Ecrire un commentaire pour aider à améliorer le contenu