Fonctions avec Python
Exercice 12  30 min
30 min  4 points.
4 points.
Un groupe de scientifiques étudie le nombre de poissons qui vivent dans un étang. Après plusieurs études de terrain, ils modélisent ce nombre par la fonction ![]() , définie sur
, définie sur ![]() [ par
[ par ![]() , où
, où ![]() est le temps, mesuré en année, écoulé depuis le
est le temps, mesuré en année, écoulé depuis le ![]() janvier
janvier ![]() \
\
On note ![]() la courbe représentative de la fonction
la courbe représentative de la fonction ![]() dans un repère.
dans un repère.
- Combien y avait-il de poissons au
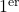 janvier 2022 ?
janvier 2022 ? - Calculer
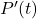 pour tout réel
pour tout réel 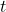 positif. En déduire le sens de variation de la fonction
positif. En déduire le sens de variation de la fonction 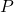 sur
sur 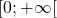 .
. - Déterminer la limite de
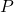 lorsque
lorsque 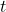 tend vers
tend vers 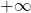 . Interpréter graphiquement cette limite.
. Interpréter graphiquement cette limite. - Interpréter dans le contexte de l’exercice la limite trouvée à la question
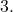
- Justifier que le nombre de poissons va dépasser 2000 individus lors d’une certaine année.
-
- Compléter la fonction Python ci-dessous afin qu’elle renvoie l’année à partir de laquelle le nombre de poissons va dépasser 2000 individus.
-
 Quelle année trouve-t-on?
Quelle année trouve-t-on?
Exercice 13
On considère la fonction ![]() définie sur
définie sur ![]() par
par ![]() . On admet que l’équation
. On admet que l’équation ![]() admet une unique solution
admet une unique solution ![]() sur l’intervalle
sur l’intervalle ![]() . On donne l’algorithme suivant:
. On donne l’algorithme suivant:
 < Exécuter pas à pas cet algorithme et compléter dans le tableau ci-dessous les valeurs prises successivement par les variCables
< Exécuter pas à pas cet algorithme et compléter dans le tableau ci-dessous les valeurs prises successivement par les variCables ![]() ,
,![]() et
et ![]() .
.

- Que représentent les variables
 et
et 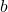 lors de la fin de l’exécution?
lors de la fin de l’exécution? - On admet que l’équation
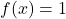 admet une deuxième unique solution
admet une deuxième unique solution 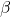 dans l’intervalle
dans l’intervalle ![Rendered by QuickLaTeX.com [5;6]](https://spe-maths.fr/wp-content/ql-cache/quicklatex.com-e305f3fb115541d12d140b745a18adf7_l3.png) et que
et que  est décroissante sur cette intervalle. Modifier le programme ci-dessous pour que les valeurs
est décroissante sur cette intervalle. Modifier le programme ci-dessous pour que les valeurs  et
et 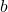 en fin d’exécution du programme soient les deux bornes d’un encadrement de
en fin d’exécution du programme soient les deux bornes d’un encadrement de 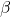 d’amplitude
d’amplitude 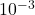 .
.
-
Tableau complété:

L’exécution donne les valeurs affectés par cet algorithme aux variables
 et
et 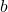 qui représentent les extrémités des intervalles emboités , encadrant par la méthode de dichotomie, la valeur de
qui représentent les extrémités des intervalles emboités , encadrant par la méthode de dichotomie, la valeur de 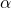 jusqu’à obtenir un intervalle d’amplitude
jusqu’à obtenir un intervalle d’amplitude 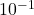 .
. - pour obtenir un encadrement de
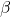 , il suffit de modifier les valeurs d’initialisation de
, il suffit de modifier les valeurs d’initialisation de  et
et 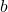 par
par 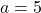
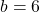 , de modifier la condition while par
, de modifier la condition while par 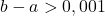 et comme la
et comme la  est décroissante remplacer la condition du if par
est décroissante remplacer la condition du if par 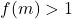 ou bien inverser les rôles de
ou bien inverser les rôles de  et
et 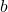 .
.
Ecrire un commentaire pour aider à améliorer le contenu