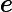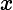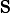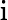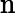Rappel de cours sur les fonctions
1.Limites de fonctions
a.Limites de référence en 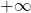 et
et 
| Limites infinies | Limites finies |
     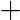           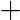     
     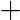   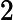         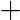   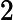   
     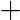   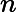         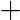   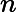    avec
avec                      
        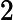 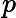 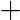 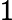            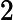 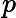 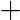 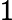    avec
avec         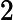 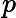            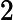 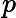    avec
avec |
     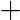  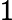          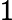   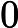      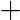  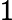          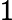   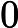
     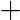                 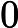      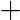  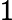  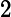         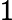  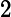  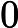
|
| Limites infinies | Limites finies |
     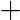  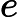          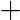  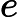    
|
|
b.Limite de référence en 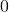
     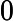 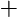 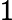          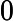 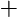 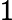    
     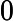  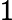          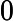  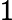    
     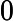 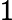  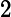         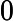 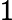  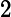   
|
Dérivée en 0 des fonctions
|
c. Limites et inégalités
|
Théorème de comparaison: Si Si alors Ces deux propriétés s’étendent pour des limites en |
Théorème dit « des gendarmes » Si 





















 et si
et si




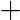

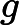




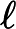





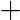

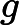




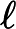 et si, pour x assez grand, f(x)≤h(x)≤g(x),
et si, pour x assez grand, f(x)≤h(x)≤g(x),
alors 




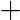






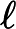





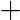






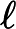 . Cette propriété s’étend est valable pour des limites en
. Cette propriété s’étend est valable pour des limites en 


 ou en un réel .
ou en un réel .
| Définition : Soit une fonction définie sur un intervalle I. Soit dans I. est continue en si et seulement si      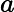               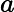          .
.  est continue sur I si et seulement si
est continue sur I si et seulement si   est continue en tout nombre
est continue en tout nombre   de I.
de I. |
|
Théorème des valeurs intermédiaires : Soit f fonction définie sur I et a et b éléments de I. il existe au moins un réel c compris entre a et b tel que : f (c) = k |
Autrement dit :
toutes « les valeurs intermédiaires » entre les deux images sont atteintes.
Corollaire du théorème des valeurs intermédiaires :Soit 
 définie sur
définie sur 









Si est continue et strictement monotone sur 








 alors :
alors :
pour tout réel compris entre 






 et
et 






 , l’équation
, l’équation 




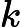





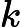 possède une et une seule solution sur l’intervalle
possède une et une seule solution sur l’intervalle 








 .
.
Remarque :
Ce corollaire peut être étendu à tout type d’intervalle.
Dans le cas de bornes ouvertes ou infinies, il faut alors remplacer les images de 
 et de par les limites de aux bornes de l’intervalle.
et de par les limites de aux bornes de l’intervalle.
Exemple : Soit la fonction 


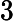

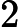


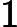



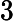

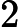


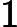 définie sur . On a est dérivable et sa dérivée
définie sur . On a est dérivable et sa dérivée 





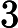

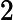

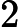






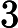

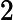

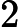 est strictement positive sur , donc
est strictement positive sur , donc 
 est strictement croissante. On a
est strictement croissante. On a 


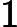



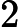



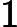



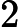 et
et 

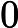


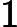


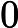


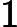 . Comme
. Comme 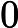



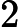
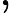

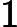

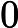



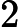
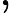

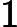
 l’équation
l’équation ![]() possède une et une seule solution dans l’intervalle ]-1,0[.
possède une et une seule solution dans l’intervalle ]-1,0[.
a. Dérivée d’une fonction composée
Théorème : Soit et deux fonctions dérivables sur ,
et 

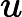

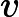


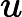

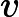 , c’est-à-dire, pour tout ,
, c’est-à-dire, pour tout , 




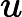

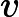









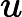

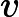



 . Alors est dérivable sur avec,
. Alors est dérivable sur avec, 


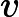

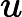


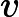



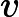

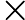
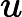


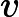 ,
,
c’est-à-dire pour tout , 





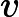




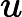


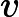










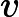




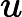


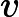



 .
.
Exemple :
Soit . Alors 

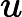

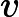


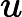

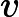 , avec
, avec 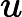





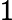
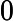
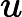





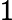
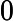 et
et 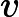





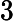

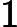

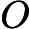
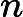


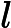
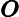
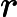
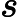
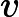





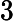

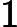

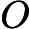
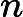


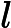
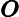
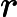
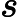 f'(x)=v'(x)\times u'(v(x))=3x^2 \times 10(x^3+1)^9 =30x^2(x^3+1)^9.
f'(x)=v'(x)\times u'(v(x))=3x^2 \times 10(x^3+1)^9 =30x^2(x^3+1)^9.
b-Convexité
Définition : Une fonction dérivable sur un intervalle I est convexe si et seulement si
sa courbe est entièrement située au dessus de chacune de ses tangente. Une fonction dérivable sur un intervalle I est concave si et seulement si sa courbe est entièrement située en dessous de chacune de ses tangentes.
Exemple :


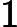


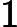 .
.On voit graphiquement que est concave sur




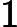





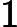
 et convexe sur
et convexe sur 
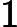
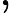




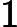
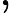


 .
.Propriété : Soit 
 une fonction dérivable deux fois sur un intervalle ]a;b[.
une fonction dérivable deux fois sur un intervalle ]a;b[.
Si 



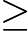
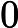




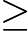
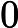 sur
sur 








 , alors f est convexe sur sur
, alors f est convexe sur sur 








 .
.
Si 




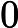





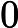 sur
sur 








 , alors est concave sur sur
, alors est concave sur sur 








 .
.
Cette propriété est valable si 






 ou
ou 






 .
.
Un point d’inflexion caractérise un changement de convexité de la courbe représentative d’une fonction continue . En un ce point, la tangente traverse la courbe.
Propriété : Soit une fonction dérivable deux fois sur un intervalle 








 .
.
Si 






 s’annule en
s’annule en 




 en changeant de signe, alors le point
en changeant de signe, alors le point 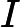








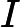







 est un point d’inflexion de la courbe représentative .
est un point d’inflexion de la courbe représentative .
Définition : La fonction logarithme népérien, notée , est la fonction définie sur 
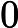





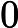



 qui,à tout réel strictement positif associe l’unique solution de l’équation d’inconnu ,
qui,à tout réel strictement positif associe l’unique solution de l’équation d’inconnu , 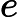
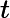


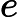
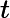

 . Ainsi, pour tout réel
. Ainsi, pour tout réel 

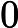


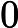 et pour tout réel
et pour tout réel 
 ,
, 


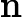



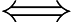
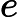
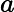





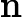



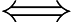
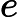
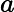

 . Ce qui donne en particulier:
. Ce qui donne en particulier: 
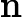

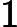


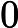

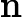

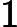


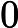 ,et
,et 
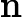

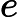


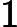

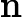

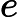


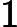 .
.
Dans un repère orthonormé, les courbes représentatives des fonctions et sont symétriques par rapport à la droite d’équation: 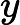


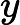

 .
.
Dérivée
- La fonction

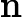

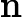 admet pour dérivée
admet pour dérivée 
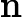





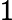


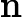





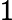
 sur
sur 
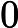





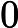



 .
. - Soit une fonction strictement positive sur un intervalle I. On a alors la dérivée :


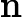

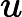




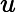
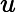


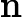

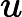




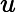
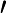
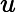
Limites
Exercices type Bac
1-Logarithme népérien, dérivation, sens de variations.
2 Limites, tableau de variations, théorème des valeurs intermédiaires
3. Fonction exponentielle, variations, équation de la tangente
4- Fonction exponentielle, drivée, coefficient directeur de la tangente.
5. Fonction exponentielle, tableau de variation, équation de la tangente.
Télécharger l’exercice 5 l’énoncé et corrigé
6 Logarithme népérien, limites, tableau de variation, nombre de solutions de l’équation 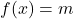 , convexité.
, convexité.
Télécharger l’exercice 6 l’énoncé et corrigé
7- Fonction logarithme népérien ,TVI, convexité, points d’inflexion.
Télécharger l’énoncé et le corrigé de l’exercice 7
8-Fonction logarithme ; dérivation, TVI.
Télécharger l’énoncé et le corrigé de l’exercice 8
9-Fonction logarithme ; dérivation, position relative de deux courbes.
Télécharger l’énoncé et le corrigé de l’exercice 9
10-Fonction exponentielle, dérivation, convexité, TVI, asymptote.
Télécharger l’énoncé et le corrigé de l’exercice 10
11-Baccalauréat spécialité maths 5 mai 2022 2 sujet 1.
Télécharger l’énoncé et le corrigé de l’exercice 11