Soit ![]() et
et ![]() deux entiers relatifs.
deux entiers relatifs.
On dit que ![]() divise
divise ![]() lorsque il existe un entier relatif
lorsque il existe un entier relatif ![]() tel que
tel que ![]() . On note
. On note ![]() .On dit aussi que
.On dit aussi que ![]() est un diviseur de
est un diviseur de ![]() ,ou encore que
,ou encore que ![]() est un multiple de
est un multiple de ![]() .
.
Théorème : Soit ![]() un entier relatif et
un entier relatif et ![]() un entier naturel non nul.
un entier naturel non nul.
Il existe alors un unique couple d’entiers relatifs ![]() tels que
tels que
![]()
Définition
Soit ![]() et
et ![]() deux entiers relatifs et
deux entiers relatifs et ![]() un entier naturel.
un entier naturel.
On dit que ![]() et
et ![]() sont congrus modulo
sont congrus modulo ![]() lorsque
lorsque ![]() et
et ![]() ont le même reste dans la division euclidienne par
ont le même reste dans la division euclidienne par ![]() .
.
On note
![]()
Corollaire
Tout nombre est congru à son reste dans la division euclidienne:
- si
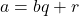 alors
alors ![Rendered by QuickLaTeX.com a\equiv r\,[q]](https://spe-maths.fr/wp-content/ql-cache/quicklatex.com-8e6b5df9dd9f5e9487bd5ad1033f4f5e_l3.png)
 est un diviseur de
est un diviseur de 

![Rendered by QuickLaTeX.com a\equiv 0\,[n]](https://spe-maths.fr/wp-content/ql-cache/quicklatex.com-807e8d58f2141092451aa34dec89430c_l3.png) (
(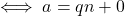 )
)- Un nombre
 est pair
est pair  si
si ![Rendered by QuickLaTeX.com a\equiv 0\,[2]](https://spe-maths.fr/wp-content/ql-cache/quicklatex.com-81f538883ac44c1e54866b4a3fdcc4ea_l3.png)
 est impair
est impair 
![Rendered by QuickLaTeX.com a\equiv1\,[2]](https://spe-maths.fr/wp-content/ql-cache/quicklatex.com-687b67a9f0021a29dccb1616dc75c7d3_l3.png)
![Rendered by QuickLaTeX.com a\equiv b\,[n] \iff a-b\equiv 0\,[n]](https://spe-maths.fr/wp-content/ql-cache/quicklatex.com-f2237a94d997b5c0d4ab96fca7e311ff_l3.png)
Congruences et opérations
Il est important de savoir comment se comportent les opérations usuelles avec les congruences.
Soit ![]() ,
, ![]() ,
, ![]() et
et ![]() des entiers relatifs, et
des entiers relatifs, et ![]() un entier naturel.
un entier naturel.
Si ![]() et
et ![]() alors
alors
![Rendered by QuickLaTeX.com a+c\equiv b+d\,[n]](https://spe-maths.fr/wp-content/ql-cache/quicklatex.com-9511a8accb7459cb146938dd8f946e3c_l3.png)
![Rendered by QuickLaTeX.com a-c\equiv b-d\,[n]](https://spe-maths.fr/wp-content/ql-cache/quicklatex.com-921949903c297114969b96062d0d9531_l3.png)
![Rendered by QuickLaTeX.com ac\equiv bd\,[n]](https://spe-maths.fr/wp-content/ql-cache/quicklatex.com-23977dc3f1321d5cc792c9f9e3227a07_l3.png)
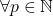 ,
, ![Rendered by QuickLaTeX.com a^p\equiv b^p\,[n]](https://spe-maths.fr/wp-content/ql-cache/quicklatex.com-359fc2dd7da45974fc0937397aaa6406_l3.png)
exercice
Soit ![]() un entier naturel. On pose
un entier naturel. On pose ![]()
Montrer que est divisible par 3.
On raisonne par disjonction de cas repose sur la décomposition de ![]() en trois cas :
en trois cas : ![]() ,
, ![]() , et
, et ![]() , où
, où ![]() est un entier naturel.
est un entier naturel.
-
- Si
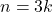 , alors :
, alors : 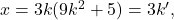 avec
avec 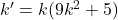 qui est un entier naturel. On constate donc que
qui est un entier naturel. On constate donc que 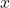 est bien divisible par 3.
est bien divisible par 3. - Si
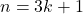 , alors :
, alors :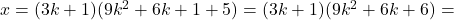
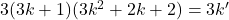 avec
avec 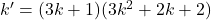 qui est entier naturel. On constate donc que
qui est entier naturel. On constate donc que 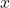 est bien divisible par 3.
est bien divisible par 3. - Si
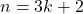 , alors :
, alors : 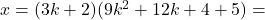
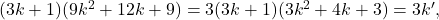 avec
avec 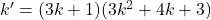 qui est un entier naturel. On constate donc que
qui est un entier naturel. On constate donc que 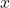 est bien divisible par 3.
est bien divisible par 3.
- Si
On a donc montré que, dans tous les cas, ![]() est divisible par 3.
est divisible par 3.