Exercices d’algèbre et géométrie
Exercices d’analyse et de probabilité
- Suites et séries numériques
- Suites et séries de fonctions
- Séries de Fourier
- Séries entières
Exercice 1
Soient  ,
, 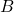 et
et 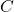 trois parties d’un ensemble
trois parties d’un ensemble  . Pour
. Pour 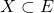 , on note
, on note 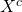 le complémentaire de
le complémentaire de 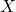 dans
dans  . Démontrer les lois de Morgan suivantes :
. Démontrer les lois de Morgan suivantes :
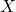 dans
dans  . Raisonner par double inclusion pour démontrer les lois de Morgan suivantes :
. Raisonner par double inclusion pour démontrer les lois de Morgan suivantes :
![]()
Corrigé
- Soit
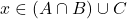 . Alors (
. Alors (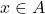 et
et 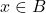 ) ou
) ou 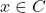 . Si
. Si 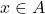 et
et 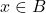 , alors
, alors 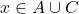 et
et 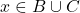 , et l’inclusion est prouvée. Sinon, c’est que
, et l’inclusion est prouvée. Sinon, c’est que 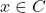 , et dans ce cas on a aussi
, et dans ce cas on a aussi 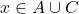 et
et 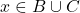 .
.
Récipoquement, si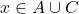 et
et 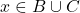 , on distingue deux cas :
, on distingue deux cas :
- Si
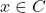 , alors
, alors 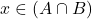 ou
ou 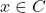 et donc
et donc 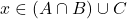 .
.
- Sinon,
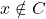 . Mais alors, puisque
. Mais alors, puisque 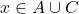 , on a
, on a 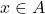 . De même, puisque
. De même, puisque 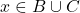 , on a
, on a 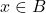 . Ceci prouve que
. Ceci prouve que 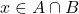 et donc
et donc 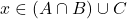 .
.
- Si
- On suppose que
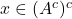 . Alors
. Alors 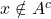 , et donc
, et donc 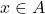 . Réciproquement, si
. Réciproquement, si 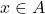 , alors
, alors 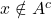 et donc
et donc 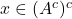 .
.
- Soit
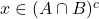 . Alors
. Alors 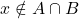 . On a donc
. On a donc 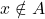 ou
ou 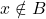 , c’est-à-dire
, c’est-à-dire
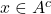 ou
ou 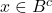 . On en déduit que
. On en déduit que 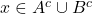 . Réciproquement, soit
. Réciproquement, soit 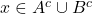 . Alors
. Alors
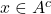 ou
ou 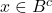 , c’est-à-dire
, c’est-à-dire 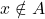 ou
ou 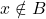 . En particulier,
. En particulier, 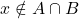 et
donc
et
donc 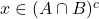 .
.
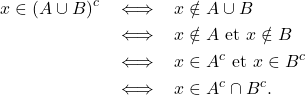
- On peut présenter aussi les raisonnements précédents sous forme d’équivalence. C’est ce que l’on fait pour ce
dernier exemple :