Exercice 1
La figure ci-dessous représente le cube ABCDEFGH d’arête de longueur 1. Montrer que les droites ![]() et
et ![]() sont orthogonales.
sont orthogonales.
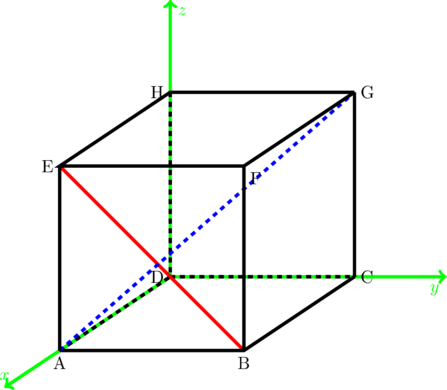
Utiliser le repère orthonormé ![]()
Coordonnées des points et des vecteurs
Les coordonnées des points A, G, E, et B sont les suivantes :
![Rendered by QuickLaTeX.com \[\begin{aligned}A & : (1, 0, 0) \\G & : (0, 1, 1) \\E & : (1, 0, 1) \\B & : (1, 1, 1)\end{aligned}\]](https://spe-maths.fr/wp-content/ql-cache/quicklatex.com-2457f132beddad57775825ac9bfd4954_l3.png)
Les coordonnées des vecteurs ![]() et
et ![]() sont respectivement :
sont respectivement :
![Rendered by QuickLaTeX.com \[\begin{aligned}\overrightarrow{AG} & : (-1, 1, 1) \\\overrightarrow{EB} & : (0, 1, -1)\end{aligned}\]](https://spe-maths.fr/wp-content/ql-cache/quicklatex.com-f4f1f0f6d6384035658419acee431bb8_l3.png)
Orthogonalité des vecteurs
Montrons que les vecteurs ![]() et
et ![]() sont orthogonaux. Deux vecteurs sont orthogonaux s’ils ont un produit scalaire nul. Le produit scalaire de
sont orthogonaux. Deux vecteurs sont orthogonaux s’ils ont un produit scalaire nul. Le produit scalaire de ![]() et
et ![]() est donné par :
est donné par :
![]()
Comme le produit scalaire est nul, les vecteurs ![]() et
et ![]() sont orthogonaux. Ainsi, les droites (AG) et (EB) sont orthogonales car elles possèdent des vecteurs directeurs orthogonaux.
sont orthogonaux. Ainsi, les droites (AG) et (EB) sont orthogonales car elles possèdent des vecteurs directeurs orthogonaux.
Exercice 2
On considère le cube ABCDEFGH d’arête de longueur 1. L’espace est muni du repère orthonormé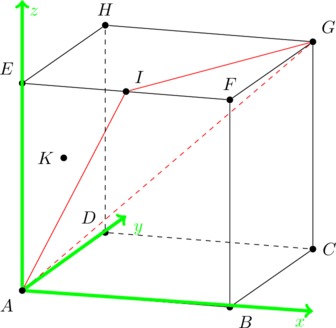
- Déterminer les coordonnées des points
 ,
,  ,
,  ,
,  ,
, 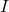 , et
, et 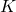 :
:
- Montrer que la droite
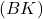 est orthogonale au plan
est orthogonale au plan 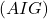 .
.
1-Les coordonnées des points E, F, A et H sont :
![]() ,
,![]() ,
, ![]() et
et ![]()
![]() est le milieu de
est le milieu de ![]() :
:![]()
![]() est le milieu de
est le milieu de ![]() :
:![]()
2-Les points ![]() ,
, ![]() et
et ![]() ne sont pas alignés, donc les vecteurs
ne sont pas alignés, donc les vecteurs ![]() et
et ![]() forment une base du plan
forment une base du plan ![]() .
.
Montrons que le vecteur ![]() est orthogonal au vecteur
est orthogonal au vecteur ![]() et au vecteur
et au vecteur ![]() en utilisant le produit scalaire.
en utilisant le produit scalaire.
Vecteur ![]() :
:
![]()
Vecteur ![]() :
:
![]()
Vecteur ![]() :
:
![]()
Produit scalaire :
![]()
![]()
Comme les produits scalaires sont nuls, le vecteur ![]() qui est un vecteur directeur de la droite
qui est un vecteur directeur de la droite ![]() est un vecteur normal au plan
est un vecteur normal au plan ![]() , Ceci montre que la droite
, Ceci montre que la droite ![]() est orthogonale au plan
est orthogonale au plan ![]() .
.
Exercice 3
On considère un cube (ABCDEFGH). L’espace est muni du repère orthonormé ![]() .
.
- Donner une représentation paramétrique de la droite (AG).
- Déterminer les positions du point M sur la droite (AG) telles que les
droites (MB) et (MD) soient orthogonales.
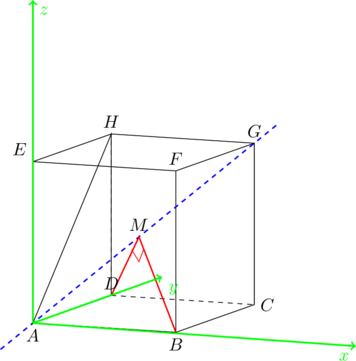
1.La droite ![]() passe par l’origine du repère
passe par l’origine du repère ![]() et a pour vecteur directeur
et a pour vecteur directeur ![]() . Une représentation paramétrique de la droite
. Une représentation paramétrique de la droite ![]() est donnée par :
est donnée par :
![Rendered by QuickLaTeX.com \[ \left\{ \begin{array}{l c l} x &=& t\\ y &=& t\\ z &=& t \end{array} \right. \quad t \in \mathbb{R} \]](https://spe-maths.fr/wp-content/ql-cache/quicklatex.com-b9e61c151d00be37bd281673ae35bebc_l3.png)
2. On cherche le point ![]() de
de ![]() tel que
tel que ![]() , c’est-à-dire
, c’est-à-dire
![]()
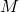 est un point de
est un point de 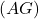 donc ses coordonnées sont de la forme
donc ses coordonnées sont de la forme 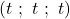 .
.- Les coordonnées de
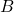 sont
sont 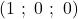 , donc
, donc 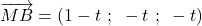 .
. - Les coordonnées de
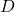 sont
sont 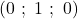 , donc
, donc 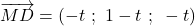 .
. - Le produit scalaire
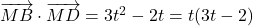 .
.
Il y a deux positions pour![Rendered by QuickLaTeX.com \[\overrightarrow{MB} \cdot \overrightarrow{MD} = 0 \iff t(3t-2) = 0 ~~\text{soit}~~ t = 0 ~~\text{ou}~~ t = \frac{2}{3}\]](https://spe-maths.fr/wp-content/ql-cache/quicklatex.com-45ab93c9a31c081373bf1f77ac33b17d_l3.png)
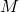 sur la droite
sur la droite 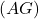 telles que
telles que 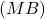 et
et 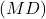 soient orthogonales :
soient orthogonales :
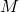 est à l’origine en A pour
est à l’origine en A pour 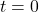 ,
,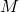 a pour coordonnées
a pour coordonnées 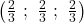 pour
pour 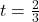 .
.
Exercice 4
On considère le cube (ABCDEFGH) illustré dans la figure ci-dessus.

Les trois points ![]() ,
, ![]() et
et ![]() vérifient :
vérifient :
![]()
On se place dans le repère orthonormé ![]() .
.
1. Donner les coordonnées des points ![]() ,
, ![]() et
et ![]() .
.
2. Démontrer que le vecteur ![]() est normal au plan
est normal au plan ![]() .
.
3. Donner une équation cartésienne du plan ![]() .
.
1.
I ![]() , J
, J ![]() , K
, K ![]() .
.
2.
On a ![]() ,
, ![]() ,
, ![]() .
.
Or ![]() et
et ![]() .
.
Le vecteur ![]() est orthogonal à deux vecteurs non colinéaires du plan (IJK) donc il est normal à ce plan.
est orthogonal à deux vecteurs non colinéaires du plan (IJK) donc il est normal à ce plan.
3.
Le vecteur (1,1,1) est normal au plan ![]() donc:
donc:
![]()
Or le point I![]() .
.
Par conséquent:![]() .
.
Le plan (IJK) a pour équation cartésienne ![]() .
.
Exercice 5
![]()
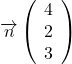 est normal au plan (ABC).
est normal au plan (ABC). ![Rendered by QuickLaTeX.com \[\left\{ \begin{array}{l c l} x &=&- 5+4t\\ y &=&0+2 t\\ z &=&1+3 t \end{array} \right. \quad t \in \mathbb{R}\]](https://spe-maths.fr/wp-content/ql-cache/quicklatex.com-7a58453f521f95c17452ab40a76188e9_l3.png)
On résout le système d’équation suivant :
![Rendered by QuickLaTeX.com \[\begin{array}{l}x=-5+4t\\y=0+2t\\z=1+3t\\4x+2y+3z-12=0\end{array}\iff\begin{array}{l}x=-5+4t\\y=0+2t\\z=1+3t\\-20+16t+4t+3+9t-12=0\end{array}\]](https://spe-maths.fr/wp-content/ql-cache/quicklatex.com-0a4061295314e51a0060a345732352bc_l3.png)
![Rendered by QuickLaTeX.com \[\iff\begin{array}{l}x=-5+4t\\y=0+2t\\z=1+3t\\t=\frac{29}{29}=1\end{array}\iff\begin{array}{l}x=-1\\y=2\\z=4\\t=1\end{array}\]](https://spe-maths.fr/wp-content/ql-cache/quicklatex.com-ba008afaec69a8a2d586e79f19dfe5d1_l3.png)
On a remplacé ![]() par
par ![]() dans l’équation paramétrique de la droite
dans l’équation paramétrique de la droite ![]() on obtient ainsi
on obtient ainsi ![]() .
.