Exercice 1
Le plan est menu d’ un repère 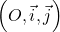 .
On donne les points
.
On donne les points 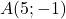 ,
, 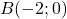 et
et 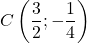 .
.
Calculer les coordonnées des vecteurs suivants :
![]() .
.
corrigé exercice 1
![]() soit
soit ![]()
![]() soit
soit ![]()
![]() soit
soit ![]()
![]() donc
donc ![]() .
.
Par conséquent ![]() d’où
d’où ![]()
Exercice 2
On considère les points 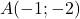 ,
, 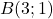 et
et 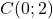 .
Calculer les coordonnées des points
.
Calculer les coordonnées des points 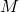 et
et 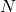 tels que
tels que 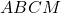 et
et 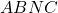 soient des parallélogrammes.
soient des parallélogrammes.
Corrigé de l’exercice 2

- On considère le point
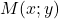 .
.
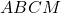 est un parallélogramme si, et seulement si,
est un parallélogramme si, et seulement si, 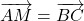 .
.
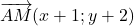 et
et 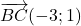 .
.
Par conséquent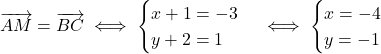 .
.
Ainsi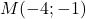 .
. - On considère le point
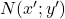 .
.
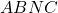 est un parallélogramme si, et seulement si,
est un parallélogramme si, et seulement si, 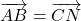 .
.
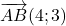 et
et 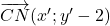 .
.
Par conséquent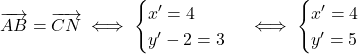 .
.
Ainsi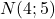 .
.
Exercice 3
On considère les points 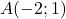 ,
, 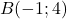 et
et 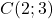 .
.
- On appelle :
–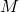 le symétrique de
le symétrique de  par rapport à
par rapport à 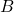 .
.
–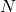 le symétrique de
le symétrique de  par rapport à
par rapport à 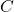 .
.
Calculer les coordonnées des points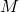 et
et 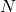 .
.

- On considère les points
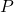 et
et 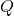 tels que
tels que 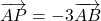 et
et 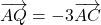 .
.
Démontrer que les droites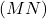 et
et 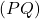 sont parallèles.
sont parallèles.

Corrigé de l’exercice 3
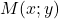 est le symétrique de
est le symétrique de  par rapport à
par rapport à 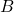 donc
donc 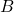 est le milieu de
est le milieu de ![Rendered by QuickLaTeX.com [AM]](https://spe-maths.fr/wp-content/ql-cache/quicklatex.com-c78f99b89fe2df28980175d379b02d7f_l3.png) .
.
Ainsi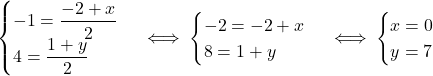
Donc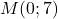 .
.

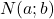 est le symétrique de
est le symétrique de  par rapport à
par rapport à 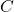 donc
donc 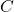 est le milieu de
est le milieu de ![Rendered by QuickLaTeX.com [AN]](https://spe-maths.fr/wp-content/ql-cache/quicklatex.com-2d2f052710d024c78209d66d4158fa3e_l3.png) .
.
Ainsi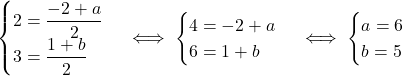
Donc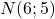 .
.

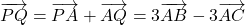
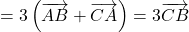 .
.
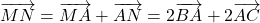
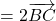 .
.
Les vecteurs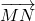 et
et 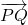 sont donc colinéaires et les droites
sont donc colinéaires et les droites 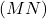 et
et 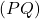 sont parallèles.
sont parallèles.

Exercice 4
On considère un parallélogramme 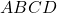 de centre
de centre 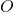 . On munit le plan du repère
. On munit le plan du repère 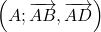 .
Déterminer dans ce repère les coordonnées des vecteurs suivants :
.
Déterminer dans ce repère les coordonnées des vecteurs suivants : 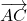 ,
, 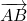 ,
, 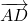 ,
, 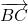 ,
, 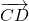 et
et 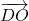 .
.

Corrigé de l’exercice 4