- Soit
 la fonction définie sur
la fonction définie sur ![Rendered by QuickLaTeX.com ]0;+\infty[](https://spe-maths.fr/wp-content/ql-cache/quicklatex.com-80243cc86f99e2d74411fff3ccaa6a1e_l3.png) par :
par : 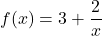 et
et 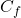 sa courbe représentative dans un repère orthonormé d’unité
sa courbe représentative dans un repère orthonormé d’unité 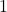 cm.
cm.
Calculer l’aire sous la courbe sur l’intervalle
sur l’intervalle ![Rendered by QuickLaTeX.com [1;4]](https://spe-maths.fr/wp-content/ql-cache/quicklatex.com-7d47d6bab2b045a261fb0309c3d5a687_l3.png) .
.
La fonction est  est continue sur
est continue sur ![Rendered by QuickLaTeX.com ]0;+\infty[](https://spe-maths.fr/wp-content/ql-cache/quicklatex.com-80243cc86f99e2d74411fff3ccaa6a1e_l3.png) en tant que somme de fonctions continues sur cet intervalle.
en tant que somme de fonctions continues sur cet intervalle.
Ainsi l’aire sous la courbe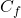 sur l’intervalle
sur l’intervalle ![Rendered by QuickLaTeX.com [1;4]](https://spe-maths.fr/wp-content/ql-cache/quicklatex.com-7d47d6bab2b045a261fb0309c3d5a687_l3.png) est :
est :
Or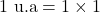 cm
cm
Donc :
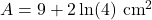
Exercice 2
Ainsi l’aire sous la courbe
![Rendered by QuickLaTeX.com <span class="ql-right-eqno"> </span><span class="ql-left-eqno"> </span><img src="https://spe-maths.fr/wp-content/ql-cache/quicklatex.com-7264c27f14ae022d6996502b2a7e6afd_l3.png" height="168" width="241" class="ql-img-displayed-equation quicklatex-auto-format" alt="\begin{align*} \mathscr{A}&=\displaystyle \int_1^4 f(x)dx \\ &=\Big[3x+2\ln(x)\Big]_1^4 \\ &=12+2\ln(4)-\left(3+2\ln(1)\right) \\ &=12+2\ln(4)-3\\ &=9+2\ln(4)\text{ u.a.}\end{align*}" title="Rendered by QuickLaTeX.com"/>](https://spe-maths.fr/wp-content/ql-cache/quicklatex.com-34d88f922619fa98c001303aedbba184_l3.png)
Or
Donc :
Soit 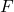 la fonction définie sur
la fonction définie sur  par
par 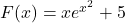 .
.
Calculer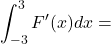 :
:
Correction
Calculer
On a :
Exercice 3
Calculer La valeur moyenne sur ![Rendered by QuickLaTeX.com [-2;1]](https://spe-maths.fr/wp-content/ql-cache/quicklatex.com-d52ba7540794bbf65e3a50e1f91136d3_l3.png) de la fonction
de la fonction  définie par
définie par 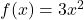 .
.
Correction
La valeur moyenne d’une fonction  sur
sur ![Rendered by QuickLaTeX.com [-2;1]](https://spe-maths.fr/wp-content/ql-cache/quicklatex.com-d52ba7540794bbf65e3a50e1f91136d3_l3.png) est donnée par la formule
est donnée par la formule
![]()
![Rendered by QuickLaTeX.com <span class="ql-right-eqno"> </span><span class="ql-left-eqno"> </span><img src="https://spe-maths.fr/wp-content/ql-cache/quicklatex.com-12c6ba3a378da4d02ea25716bf7205aa_l3.png" height="199" width="190" class="ql-img-displayed-equation quicklatex-auto-format" alt="\begin{align*} m&=\dfrac{1}{1-(-2)}\displaystyle \int_{-2}^1 3x^2dx \\ &=\dfrac{1}{3}\Big[x^3\Big]_{-2}^1 \\ &=\dfrac{1^3-(-2)^3}{3} \\ &=\dfrac{1+8}{3} \\ &=3\end{align*}" title="Rendered by QuickLaTeX.com"/>](https://spe-maths.fr/wp-content/ql-cache/quicklatex.com-e39f095eb22fd19229e9f81b759dacd4_l3.png)
L’aire du domaine situé entre
a.
b.
c.
d.
Correction Question 6
![]() et
et ![]() sont deux fonctions continues sur
sont deux fonctions continues sur ![]() donc
donc ![]() et
et ![]() le sont aussi.
le sont aussi.
Il faut déterminer le signe de ![]() sur
sur ![]() .
.
Pour tout réel ![]() on a :
on a :
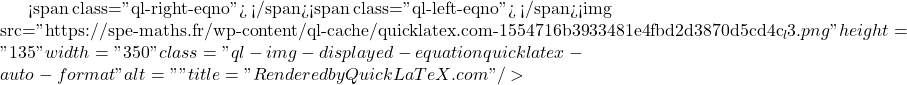
Par conséquent
Ainsi l’aire du domaine situé entre
![Rendered by QuickLaTeX.com <span class="ql-right-eqno"> </span><span class="ql-left-eqno"> </span><img src="https://spe-maths.fr/wp-content/ql-cache/quicklatex.com-f37184b4765d9cce63541e29bbe22155_l3.png" height="285" width="315" class="ql-img-displayed-equation quicklatex-auto-format" alt="\begin{align*} \mathscr{A}&=\displaystyle \int_{-5}^2 \left(g(x)-f(x)\right)dx \\ &=\int_{-5}^2\left(-2x^2-6x+20\right) dx \\ &=\left[-\dfrac{2}{3}x^3-3x^2+20x\right]_{-5}^2 \\ &=-\dfrac{16}{3}-12+40-\left(\dfrac{250}{3}-75-100\right) \\ &=-\dfrac{266}{3}+203\\ &=\dfrac{343}{3}\end{align*}" title="Rendered by QuickLaTeX.com"/>](https://spe-maths.fr/wp-content/ql-cache/quicklatex.com-08a041c6ba2c5e40569f792cae489bd7_l3.png)
Réponse b. et c.
a.
b.
c.
d.
Les primitives sur
Si
De plus on a
Ainsi les primitives sur
Réponse a. et b.
a.
b.
c.
d.
Correction Question 8
On note  la fonction définie sur
la fonction définie sur  par
par 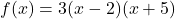 .
.
Ainsi
La fonction est continue sur
est continue sur  en tant que polynôme.
en tant que polynôme.
Les primitives de la fonction sont donc les fonctions
sont donc les fonctions 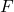 définies par
définies par 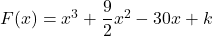 où
où 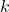 est un réel.
est un réel.
Si on développe l’expression a. on obtient un polynôme de degré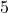 . Cette réponse ne convient donc pas.
. Cette réponse ne convient donc pas.
Si on développe l’expression d. on obtient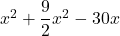 .
.
Réponse c. et d.

Ainsi
La fonction
Les primitives de la fonction
Si on développe l’expression a. on obtient un polynôme de degré
Si on développe l’expression d. on obtient
Réponse c. et d.
[collapse]
La valeur moyenne de
a.
b.
c.
d.
La valeur moyenne de ![]() sur
sur ![]() est :
est :
![Rendered by QuickLaTeX.com <span class="ql-right-eqno"> </span><span class="ql-left-eqno"> </span><img src="https://spe-maths.fr/wp-content/ql-cache/quicklatex.com-f5a45eecdfc816aafa735bd76af477fb_l3.png" height="177" width="198" class="ql-img-displayed-equation quicklatex-auto-format" alt="\begin{align*} m&=\displaystyle \dfrac{1}{0-(-2)}\int_{-2}^0 f(x)dx \\ &=\dfrac{1}{2}\left[x+e^{-x^2/2}\right]_{-2}^0 \\ &=\dfrac{1}{2}\left(1-\left(-2+e^{-2}\right)\right) \\ &=\dfrac{3-e^{-2}}{2}\end{align*}" title="Rendered by QuickLaTeX.com"/>](https://spe-maths.fr/wp-content/ql-cache/quicklatex.com-7e63f45fca069293c89ac23957eb0ad0_l3.png)
Réponse a.
a.
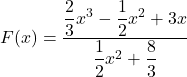
b.
c.
d.
Correction Question 10
Pour tout réel 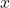 appartenant à
appartenant à ![Rendered by QuickLaTeX.com ]0;+\infty[](https://spe-maths.fr/wp-content/ql-cache/quicklatex.com-80243cc86f99e2d74411fff3ccaa6a1e_l3.png) on a :
on a :
Ainsi les primitives de la fonction sont définies par
sont définies par 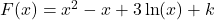 où
où 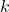 est un réel.
est un réel.
Réponse d.

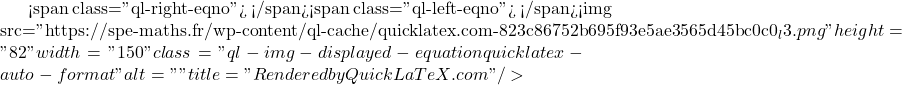
Ainsi les primitives de la fonction
Réponse d.
a.
b.
c.
d.
Correction Question 11 On a :
![Rendered by QuickLaTeX.com <span class="ql-right-eqno"> </span><span class="ql-left-eqno"> </span><img src="https://spe-maths.fr/wp-content/ql-cache/quicklatex.com-a27adc7d15d9782c991f4db6850946df_l3.png" height="187" width="306" class="ql-img-displayed-equation quicklatex-auto-format" alt="\begin{align*} I&=\displaystyle \int_1^4\left(2x-1+\dfrac{3}{x}\right)dx \\ &=\left[x^2-x+3\ln(x)\right]_1^4 \\ &=16-4+3\ln(4)-\left(1^2-1+3\ln(1)\right) \\ &=12+3\ln(4)\\ &=12+3\ln\left(2^2\right) \\ &=12+6\ln(2)\end{align*}" title="Rendered by QuickLaTeX.com"/>](https://spe-maths.fr/wp-content/ql-cache/quicklatex.com-9dad35793bb57b7b4c55684578f3c70c_l3.png)
Réponse a.
[collapse]