\tableofcontents
Le plan est rapport un repère orthonormal ![]()
\section{Forme algébrique d’un nombre complexe}
\subsection{Définitions}
\begin{itemize}
\item L’ensemble des nombres de la forme ![]() , où
, où ![]() et
et ![]() sont des réels et
sont des réels et ![]() est tel que
est tel que ![]() , est appelé ensemble des nombres complexes. On le note
, est appelé ensemble des nombres complexes. On le note ![]() .
.
Les propriétés des opérations addition et multiplication dans ![]() se prolongent dans
se prolongent dans ![]() .
.
\item L’écriture ![]() est la forme algébrique du nombre complexe
est la forme algébrique du nombre complexe ![]() .
.
![]() est la partie réelle de
est la partie réelle de ![]() ,
, ![]() sa partie imaginaire.
sa partie imaginaire.
On note ![]() .
.
![]() est une partie de
est une partie de ![]() ,
, ![]() contient les nombres complexes dont la partie imaginaire
contient les nombres complexes dont la partie imaginaire ![]() est nulle.
est nulle.
\item Tout nombre complexe dont la partie réelle est nulle est appelé nombre imaginaire pur.
\end{itemize}
\subsection{Somme, produit et inverse}
Soient ![]() et
et ![]() deux nombres complexes.
deux nombres complexes.
![]()
\subsection{équation dans ![]() }
}
Soit l’équation ![]() . où
. où ![]() et
et ![]() sont des réels,
sont des réels, ![]() non nul,
non nul, ![]() est le discriminant.
est le discriminant.
\begin{itemize}
\item Si ![]() l’équation admet un unique solution :
l’équation admet un unique solution :![]() .
.
\item Si ![]() l’équation admet deux solutions réelles :
l’équation admet deux solutions réelles :![]() et
et ![]() .
.
\item Si ![]() l’équation admet deux solutions complexes :
l’équation admet deux solutions complexes :![]() et
et ![]() .
.
\end{itemize}
\section{Interprétation géométrique d’un nombre complexe}
\subsection{Définitions}
%%\begin{minipage}{12cm}
Soit M un point de coordonnées ![]() .\\
.\\
Le nombre complexe ![]() est appelé affixe du point M.\\
est appelé affixe du point M.\\
Le point M est appelé image du nombre complexe ![]() .\\
.\\
On note M![]() le point d’affixe
le point d’affixe ![]() .
.
Remarques
\begin{itemize}
\item Le nombre complexe ![]() est aussi l’affixe du vecteur
est aussi l’affixe du vecteur ![]() .
.
\item Le vecteur ![]() est aussi l’image du nombre complexe
est aussi l’image du nombre complexe ![]() .
.
\item Le plan muni du repère orthonormal direct ![]() est appel plan complexe.
est appel plan complexe.
\end{itemize}
%\end{minipage}
Ici image bis
\subsection{Somme et opposé}
%\begin{minipage}{10cm}
\begin{enumerate}
\item Soit M et P deux points d’affixe ![]() et
et ![]() .\\
.\\
Le point S défini par ![]() a pour affixe
a pour affixe ![]() .
.
\item Le point N défini par ![]() a pour affixe
a pour affixe ![]() .
.
\item l’affixe du vecteur ![]() est
est ![]() .
.
\end{enumerate}
%\end{minipage}
lci image 1
\subsection{Module d’un nombre complexe}
\subsubsection{Définition}
Soit M un point du plan d’affixe ![]() . On appelle module du nombre complexe
. On appelle module du nombre complexe ![]() la distance
la distance ![]() . On le note
. On le note ![]() .
.
\subsubsection{Propriétés}
Soit ![]() et
et ![]() deux points d’affixes respectives les nombres complexes
deux points d’affixes respectives les nombres complexes ![]() et
et ![]() .
.
\begin{description}
\item[![]() ] Si
] Si ![]() alors
alors ![]()
\item[![]() ]
] ![]()
\item[![]() ]
] ![]() .
.
\item[![]() ]
] ![]()
\item[![]() ]
] ![]() entier naturel.
entier naturel.
\item[![]() ]
] ![]() .
.
\end{description}
\section{Forme trigonométrique d’un nombre complexe}
\subsection{Définition d’un argument d’un nombre complexe}
%%\begin{minipage}{12cm}
Soit M un point d’affixe le nombre complexe ![]() non nul.\\
non nul.\\
On appelle argument de ![]() tous les réels
tous les réels ![]() , mesure en radians de l’angle
, mesure en radians de l’angle![]() .\\ On note
.\\ On note ![]() ou
ou ![]() (modulo
(modulo ![]() ).
).
Autrement dit, un nombre complexe non nul a une infinité d’arguments.\\ Si ![]() est l’un d’entre eux, tout autre argument de
est l’un d’entre eux, tout autre argument de ![]() s’écrit
s’écrit ![]() \\ On dit aussi qu’un argument de
\\ On dit aussi qu’un argument de ![]() est défini modulo
est défini modulo ![]() .
.
%\end{minipage}
Ici image 2
\subsection{Remarque}
Le nombre complexe 0 n’a pas d’argument car la définition ![]() suppose
suppose ![]() .
.
\subsection{Propriétés}
%%\begin{minipage}{12cm}
\begin{enumerate}
\item Si ![]() est un rel strictement positif alors
est un rel strictement positif alors ![]() .
.
\item Si ![]() est un rel strictement négatif alors
est un rel strictement négatif alors ![]() .
.
\item Si ![]() est un imaginaire pur non nul alors
est un imaginaire pur non nul alors ![]() .
.
\item Si ![]() alors
alors ![]()
\item Si ![]() alors
alors ![]() .
.
\end{enumerate}
%%\end{minipage}
ici image 3
\subsection{Définition de la forme trigonométrique d’un nombre complexe}
%\begin{minipage}{12cm}
Tout nombre complexe ![]() non nul, de module
non nul, de module ![]() et dont un argument est
et dont un argument est ![]() , peut s’écrire
, peut s’écrire ![]() \\
\\
Cette écriture est appelé forme trigonométrique du nombre complexe ![]() .
.
\subsection{Formes trigonométrique et algébrique}
Soit ![]() un nombre complexe non nul.\\
un nombre complexe non nul.\\
On a ![]() \\avec
\\avec ![]() et
et ![]() .
.
Réciproquement:\\
si ![]() alors
alors ![]() et
et ![]() .
.
%%\end{minipage}
Ici image 4
\subsection{L’argument du produit est égal à la somme des arguments.}
Soit ![]() de module
de module ![]() et d’argument
et d’argument ![]() ,
, ![]() de module
de module ![]() et d’argument
et d’argument ![]() deux nombres complexes non nuls.
deux nombres complexes non nuls.
![]()
\subsection{Formule de Moivre.}
Soit ![]() et
et ![]() un entier naturel. On a
un entier naturel. On a ![]() .
.
Autrement dit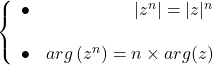
\section{Forme exponentielle d’un nombre complexe}
\begin{itemize}
\item Le nombre complexe de module 1 et dont un argument est ![]() est not
est not ![]() .
.
\item Si ![]() est un nombre complexe de module
est un nombre complexe de module ![]() et d’argument
et d’argument ![]() on écrit
on écrit ![]() .
.
\end{itemize}
Autrement dit ![]()
\subsection{Remarque}
\begin{enumerate}
\item ![]()
\item ![]()
\item Formule de Moivre :![]() .
.
\end{enumerate}
\subsection{Formules d’Euler}![]()
donne 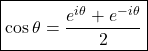 et
et 
\section{ Racine n-ième d’un nombre complexe}
Si ![]() est un nombre complexe, on appelle racine
est un nombre complexe, on appelle racine ![]() -ième de
-ième de ![]() tout nombre complexe
tout nombre complexe ![]() tel que
tel que ![]()
<ul>
<li>Si ![]() est nul, alors il admet exactement une racine
est nul, alors il admet exactement une racine ![]() -ième, lui-même.
-ième, lui-même.
<li>Si ![]() est non-nul, il admet exactement
est non-nul, il admet exactement ![]() racines
racines ![]() -ièmes distinctes.
-ièmes distinctes.
Pour les déterminer, on utiliser l’écriture trigonométrique de ![]() : si
: si ![]() , ses racines
, ses racines ![]() -ièmes sont
-ièmes sont
![]()
</ul>
\subsection{Racines n-ièmes de l’unité}
On appelle racine
tous les nombres complexes
Ce sont donc les nombres complexes
s’écrivant
Pour un entier
Dans la figure ci-dessous, les racines 5-ièmes de l’unité sont les sommets d’un pentagone régulier
ici image 5