Cours PRODUIT SCALAIRE
Exercice 1
Dans un repère orthonormal 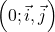 ,
calculer le produit scalaire
,
calculer le produit scalaire 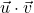 dans chacun des cas
suivants,
et en déduire une valeur de l’angle
dans chacun des cas
suivants,
et en déduire une valeur de l’angle
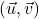 à
à 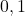 degré près.
degré près.
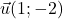 et
et 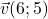
-
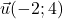 et
et 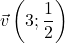
-
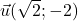 et
et 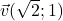 .
.
Corrigé de l’exercice 1
Exercice 2
On se place dans un repère orthonormal 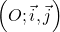 .
Dans chacun des cas, déterminer la valeur de
.
Dans chacun des cas, déterminer la valeur de 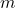 pour que les vecteurs
pour que les vecteurs
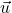 et
et 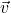 soient orthogonaux.
soient orthogonaux.
-
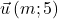 et
et 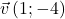
-
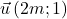 et
et 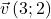
-
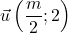 et
et 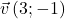
-
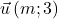 et
et 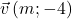
Exercice 3
Dans un un repère orthonormal 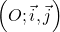 ,
on considère les points
,
on considère les points
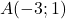 ,
, 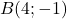 et
et 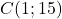 .
Les droites
.
Les droites 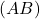 et
et 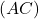 sont-elles perpendiculaires ?
sont-elles perpendiculaires ?