Suites avec Python
Exercice1
Le capital doublera au bout de 18 ans.
Exercice 2
Exercice 3
Ecrire un programme Python qui calcule les termes de la suite ![]() définie par l’expression
définie par l’expression
![]() . Afficher en particulier les termes
. Afficher en particulier les termes ![]() et
et ![]()
Qu’observe-t-on pour des valeurs de plus en plus grandes de n ?
On remarque que pour des valeurs de plus en plus grandes de n, les termes de la suite ![]() se rapprochent de 5.
se rapprochent de 5.
Exercice 4
Soit ![]() la suite définie par
la suite définie par ![]() et pour tout
et pour tout ![]() ,
, ![]() .
.
On admet que la suite ![]() est positive et croissante.
est positive et croissante.
Ecrire un programme langage Python qui donne la plus petite valeur de ![]() à partir de laquelle
à partir de laquelle ![]() dépasse 12000.
dépasse 12000.
Le programme affiche la valeur de n=41. Vous pouvez modifier le programme pour afficher la valeur de ![]() correspondante en utilisant print(n,u(n) ) à l’extérieur de la boucle while ou bien afficher toutes les valeurs de
correspondante en utilisant print(n,u(n) ) à l’extérieur de la boucle while ou bien afficher toutes les valeurs de ![]() avec print(n,u(n) ) à l’interieur de la boucle.
avec print(n,u(n) ) à l’interieur de la boucle.
Exercice 5
On considère la suite ![]() définie par
définie par ![]() et pour tout entier naturel
et pour tout entier naturel ![]() par
par ![]() .
.
On admet que cette suite est positive et tend vers 0. Ecrire un programme Python qui affiche la plus petite valeur de ![]() pour laquelle
pour laquelle ![]() .
.
Les termes de la suites sont positifs, le programme commence le calcule de ces termes par u=1, et continue tant que ![]() et s’arrête lorsque le terme u devient inférieur ou égal à 0,001 et renvoie le rang N correspondant.
et s’arrête lorsque le terme u devient inférieur ou égal à 0,001 et renvoie le rang N correspondant.
Afficher les termes de la suite avec l’instruction :
print " n =",n,"u=",u
à l’intérieur de la boucle while pour voir que u diminue jusqu’à devenir ![]() .
.
Exercice 6
On considère la suite définie par : pour tout entier naturel ![]() ,
, ![]() .
.
- Exprimer
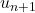 en fonction de
en fonction de 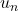 pour tout naturel
pour tout naturel  .
. - Donner le sens de variation de
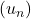 ainsi que sa limite.
ainsi que sa limite. - Ecrire un programme en Python permettant de déterminer la plus petite valeur
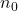 telle que
telle que 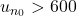 . Afficher la valeur de
. Afficher la valeur de 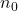
- Pour tout naturel
 :
: 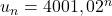 .
.
On reconnaît ici la formule explicite donnant le terme de rang d’une suite géométrique de raison 1,02 de premier terme
d’une suite géométrique de raison 1,02 de premier terme 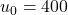 . Par conséquent, on a la formule de récurence suivante : pour tout naturel
. Par conséquent, on a la formule de récurence suivante : pour tout naturel  :
: 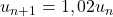 .
. - Comme
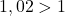 , alors la suite
, alors la suite 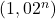 est strictement croissante. Et comme
est strictement croissante. Et comme 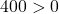 , la suite
, la suite 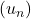 est également strictement croissante. Par ailleurs: Comme
est également strictement croissante. Par ailleurs: Comme 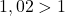 , on a:
, on a: 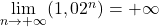 Or
Or 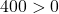 . Donc
. Donc 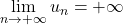
- Deux algorithmes possibles :
- Un premier algorithme qui utilise la formule de récurrence, la variable N contient la valeur
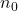 cherchée :
cherchée :
- Un deuxième algorithme qui utilise la formule explicite :
Exercice 7  12 minutes
12 minutes  1,2 points
1,2 points
On considère la suite ![]() u_n
u_n ![]() définie par
définie par ![]() et
et ![]() .
.
Recopier le script python ci-dessous et compléter les lignes 3 et 6 pour que liste(k) prenne en paramètre un entier naturel k et renvoie la liste des premières valeurs de la suite ![]() u_n
u_n ![]() de
de ![]() à
à ![]() .
.

Avec l’istruction print liste(5) afficher une liste de 6 premiers termes de la suite ![]() . Vérifier que les termes de
. Vérifier que les termes de ![]() sont les inverses des entiers naturels non nuls.
sont les inverses des entiers naturels non nuls.
Probabilités avec Python
Exercice 8
Une roue de loterie est formée de 10 cases : 2 cases rouges et 8 cases noires. Si on obtient une case rouge, on gagne 5 €, sinon on perd 1 €. X est la variable aléatoire qui donne le gain du joueur.
- Déterminer la loi de probabilité de X
- Écrire en langage Python :
- une fonction Gain qui simule la variable aléatoire X ;
- une fonction Moyenne qui calcule et renvoie pour résultat la moyenne d’un échantillon de taille n de X.
c. Tester ces deux fonctions.
a. ![]() et
et ![]()
b. Voici les fonctions Gain et Moyenne écrites en langage Python.
c. Test : La fonction Gain() affiche 5 ou -1 et pour la fonction Moyenne on a pris l’exemple d’un échantillon de taille 1000.
Exercice 9
On dispose d’un de équilibré à 6 faces et de deux urnes : l’urne ![]() contient deux boules vertes et 3 rouges, et l’urne
contient deux boules vertes et 3 rouges, et l’urne ![]() contient 1 boule verte et deux rouges. On lance le dé et si le résultat est 1 ou 2 alors on tire une boule dans l’urne
contient 1 boule verte et deux rouges. On lance le dé et si le résultat est 1 ou 2 alors on tire une boule dans l’urne ![]() , sinon on tire dans l’urne
, sinon on tire dans l’urne ![]() . On considère que la partie est gagnante si on tire une boule verte.
. On considère que la partie est gagnante si on tire une boule verte.
- Écrire un algorithme en Python permettant de simuler cette partie.
- Modifier cet algorithme pour qu’il simule n parties et compte le nombre de parties gagnantes.
- Voici un programme Python pour simuler une partie
2.Voici un programme Python pour simuler n parties
b. On trouve l’année 2030
Exercice 10
Ecrire un programme Python. avec :
- une fonction saut(n) qui retourne l’abscisse du point d’arrivée à l’issue de la marche de n sauts.
- Ensuite une fonction cible(x,n) qui retournera la fréquence de fois où l’on est arrivé à l’origine à la fin de la marche sur les n sauts effectués.
Fonctions avec Python
Exercice 11
Un groupe de scientifiques étudie le nombre de poissons qui vivent dans un étang. Après plusieurs études de terrain, ils modélisent ce nombre par la fonction ![]() , définie sur
, définie sur ![]() [ par
[ par ![]() , où
, où ![]() est le temps, mesuré en année, écoulé depuis le
est le temps, mesuré en année, écoulé depuis le ![]() janvier
janvier ![]() \
\
On note ![]() la courbe représentative de la fonction
la courbe représentative de la fonction ![]() dans un repère.
dans un repère.
- Combien y avait-il de poissons au
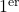 janvier 2022 ?
janvier 2022 ? - Calculer
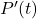 pour tout réel
pour tout réel 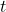 positif. En déduire le sens de variation de la fonction
positif. En déduire le sens de variation de la fonction 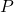 sur
sur 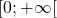 .
. - Déterminer la limite de
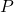 lorsque
lorsque 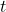 tend vers
tend vers 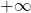 . Interpréter graphiquement cette limite.
. Interpréter graphiquement cette limite. - Interpréter dans le contexte de l’exercice la limite trouvée à la question
- Justifier que le nombre de poissons va dépasser 2000 individus lors d’une certaine année.
-
- Compléter la fonction Python ci-dessous afin qu’elle renvoie l’année à partir de laquelle le nombre de poissons va dépasser 2000 individus.
-
 Quelle année trouve-t-on?
Quelle année trouve-t-on?
b. On trouve l’année 2030
