Exercice 1 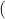 Événements indépendants
Événements indépendants 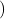
-
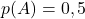 et
et 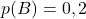
-
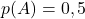 et
et 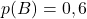
-
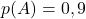 et
et 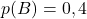
-
Les événements
 et
et 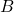 sont indépendants. Donc
sont indépendants. Donc 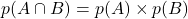 .
.
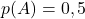 et
et 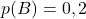 Donc :
Donc :
![Rendered by QuickLaTeX.com \[<span class="ql-right-eqno"> </span><span class="ql-left-eqno"> </span><img src="https://spe-maths.fr/wp-content/ql-cache/quicklatex.com-111190201555a85dea3708e28e36b592_l3.png" height="71" width="188" class="ql-img-displayed-equation quicklatex-auto-format" alt="\begin{align*} p(A\cap B)&=p(A)\times p(B) \\ &=0,5\times 0,2\\ &=0,1\end{align*}" title="Rendered by QuickLaTeX.com"/>\]](https://spe-maths.fr/wp-content/ql-cache/quicklatex.com-306f6d893e9239d8fae0cfa36b4bef11_l3.png)
-
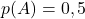 et
et 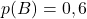 Donc :
Donc :
![Rendered by QuickLaTeX.com \[<span class="ql-right-eqno"> </span><span class="ql-left-eqno"> </span><img src="https://spe-maths.fr/wp-content/ql-cache/quicklatex.com-62de4b6c10ffd5a47d17b0df26e660ca_l3.png" height="71" width="188" class="ql-img-displayed-equation quicklatex-auto-format" alt="\begin{align*} p(A\cap B)&=p(A)\times p(B) \\ &=0,5\times 0,6\\ &=0,3\end{align*}" title="Rendered by QuickLaTeX.com"/>\]](https://spe-maths.fr/wp-content/ql-cache/quicklatex.com-bb33c0c19e9d0a0611e32ea19a39a373_l3.png)
-
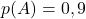 et
et 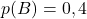 Donc :
Donc :
![Rendered by QuickLaTeX.com \[<span class="ql-right-eqno"> </span><span class="ql-left-eqno"> </span><img src="https://spe-maths.fr/wp-content/ql-cache/quicklatex.com-88a52ca28f2f19a0b4ab272afefe1126_l3.png" height="71" width="188" class="ql-img-displayed-equation quicklatex-auto-format" alt="\begin{align*} p(A\cap B)&=p(A)\times p(B) \\ &=0,9\times 0,4\\ &=0,36\end{align*}" title="Rendered by QuickLaTeX.com"/>\]](https://spe-maths.fr/wp-content/ql-cache/quicklatex.com-42ce0cf3bf11f7926d3c315c6196d36a_l3.png)
Exercice 2  Probabilité conditionnelle
Probabilité conditionnelle 
Si un enfant qui aime les oranges est choisi au hasard, quelle est la probabilité qu’il aime aussi les bananes ?
- L’événement O : « l’enfant aime les oranges »;
- L’événement B : « l’enfant aime les bananes ».
-
D’après l’énoncé on a
On cherche la probabilité conditionnelle
![]()
Exercice 3  Probabilité conditionnelle
Probabilité conditionnelle 
- H l’événement : « personnes ayant une assurance habitation »,
- V l’événement V : « personnes ayant une assurance voiture ».
Exercice 4  Probabilité conditionnelle
Probabilité conditionnelle 
![Rendered by QuickLaTeX.com \[\begin{array}{|c|c|c|c|} \hline & \text{ Mobile } & \text{Tablette} & \text{Total} \\\\ \hline \text{A} &20 & 10 & 30\\\\ \hline \text{B} & 30 & 40 & 70\\\\ \hline \text{Total} & 50 & 50 & 100 \\\\ \hline \end{array}\]](https://spe-maths.fr/wp-content/ql-cache/quicklatex.com-dba22490d9f63c4bea15a66e970eed08_l3.png)
Si une personne est choisie au hasard dans le groupe, quelle est la probabilité qu’elle
- a acheté la marque B ?
- a acheté un téléphone mobile de la marque B ?
- a acheté un téléphone mobile sachant qu’elle a acheté la marque B ?
- L’événement M: « Achat d’un téléphone mobile »
- L’événement T : « Achat d’une tablette »
- L’événement A : « Achat de la marque A »
- L’événement B : « Achat de la marque B »
- 70 personnes sur un total de 100 ont acheté la marque B ; Par conséquent
![Rendered by QuickLaTeX.com \[P(B) = 70/100 = 0,7\]](https://spe-maths.fr/wp-content/ql-cache/quicklatex.com-bc50fbc62311d5fe25ce79e4702a92c6_l3.png)
- Au total, 30 personnes sur 100 ont acheté un mobile de la marque B
![Rendered by QuickLaTeX.com \[P(M \cap B) = 30/100 = 0,3\]](https://spe-maths.fr/wp-content/ql-cache/quicklatex.com-2c3544fbdb7c4b2286db812cb880da63_l3.png)
La probabilité conditionnelle![Rendered by QuickLaTeX.com \[P_B(M) = \dfrac{P(M \cap B)}{P(B)} = 0,3/0,7 = 3/7\]](https://spe-maths.fr/wp-content/ql-cache/quicklatex.com-89ffc7399ac31995c8e856d86f140779_l3.png)
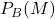 peut également être trouvée en restreignant l’univers à la marque B.
Il y a 30 téléphones mobiles sur un total de 70 de marque B ; Par conséquent
peut également être trouvée en restreignant l’univers à la marque B.
Il y a 30 téléphones mobiles sur un total de 70 de marque B ; Par conséquent
![Rendered by QuickLaTeX.com \[P_B(M) = \dfrac{30}{70} = 3/7\]](https://spe-maths.fr/wp-content/ql-cache/quicklatex.com-949e7c995e617295bed84b3e72476fff_l3.png)
Exercice 5  Événements indépendants
Événements indépendants 
-
On tire au hasard une carte dans un jeu de
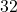 cartes.
cartes.
 est l’événement « la carte tirée est un roi » et
est l’événement « la carte tirée est un roi » et 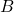 est l’événement « la carte tirée est un trèfle ».
est l’événement « la carte tirée est un trèfle ».
-
On tire au hasard une carte dans un jeu de
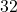 cartes.
cartes.
 est l’événement « la carte tirée est rouge » et
est l’événement « la carte tirée est rouge » et 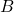 est l’événement « la carte tirée est un cœur ».
est l’événement « la carte tirée est un cœur ».
-
On lance un dé cubique non truqué dont les faces sont numérotées de
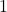 à
à 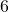 .
.
 est l’événement « le nombre obtenu est pair » et
est l’événement « le nombre obtenu est pair » et 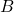 est l’événement « le nombre obtenu est un multiple de
est l’événement « le nombre obtenu est un multiple de 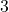 ».
».
-
On lance un dé cubique non truqué dont les faces sont numérotées de
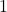 à
à 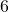 .
.
 est l’événement « le nombre obtenu est inférieur ou égal à
est l’événement « le nombre obtenu est inférieur ou égal à 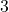 » et
» et 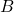 est l’événement « le nombre obtenu est un multiple de
est l’événement « le nombre obtenu est un multiple de 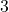 ».
».
-
On lance un dé cubique non truqué dont les faces sont numérotées de
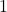 à
à 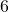 .
.
 est l’événement « le nombre obtenu est pair » et
est l’événement « le nombre obtenu est pair » et 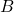 est l’événement « le nombre obtenu est inférieur ou égal à
est l’événement « le nombre obtenu est inférieur ou égal à 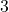 ». Les évènements
». Les évènements  et
et 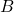 sont-ils indépendants?
sont-ils indépendants?
- Il y a
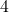 rois dans un jeu de
rois dans un jeu de 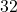 cartes. Donc
cartes. Donc 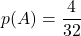 soit
soit 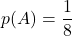 .
Un quart des cartes sont des trèfle. Donc
.
Un quart des cartes sont des trèfle. Donc 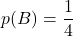 .
Il n’y a qu’un seul roi de trèfle dans le jeu. Par conséquent
.
Il n’y a qu’un seul roi de trèfle dans le jeu. Par conséquent 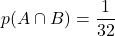 .
Ainsi:
.
Ainsi:
Les événements![Rendered by QuickLaTeX.com \[p(A)\times p(B)=\dfrac{1}{8}\times \dfrac{1}{4} =\dfrac{1}{32}=p(A\cap B)\]](https://spe-maths.fr/wp-content/ql-cache/quicklatex.com-fcef5a374dee0504251ca3c803486bea_l3.png)
 et
et 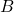 sont indépendants.
La moitié des cartes du jeu sont rouges. Donc
sont indépendants.
La moitié des cartes du jeu sont rouges. Donc -
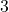 nombres sont pairs. Donc
nombres sont pairs. Donc
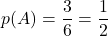 . Seuls
. Seuls 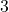 et
et 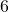 sont des multiples de
sont des multiples de 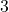 . Donc :
. Donc :
Le seul nombre pair qui soit un multiple de![Rendered by QuickLaTeX.com \[p(B)=\dfrac{2}{6} =\dfrac{1}{3}\]](https://spe-maths.fr/wp-content/ql-cache/quicklatex.com-17912c58c5c55dacb49d6e277f4e4997_l3.png)
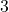 est
est 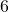 . Donc
. Donc 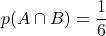 .
Ainsi:
.
Ainsi:
Les événements![Rendered by QuickLaTeX.com \[p(A)\times p(B)=\dfrac{1}{2}\times \dfrac{1}{3}=\dfrac{1}{6} =p(A\cap B)\]](https://spe-maths.fr/wp-content/ql-cache/quicklatex.com-5cb6aacbf9404a10494e1494983aba67_l3.png)
 et
et 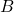 sont indépendants.
sont indépendants.
-
Les nombres inférieurs ou égaux à
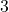 sont
sont 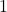 ,
,  et
et 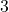 .
Donc :
.
Donc :
Seuls![Rendered by QuickLaTeX.com \[p(A)=\dfrac{3}{6}=\dfrac{1}{2}\]](https://spe-maths.fr/wp-content/ql-cache/quicklatex.com-ff63e9dfb75b8eebaf120d2611858488_l3.png)
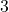 et
et 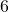 sont des multiples de
sont des multiples de 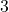 . Donc :
. Donc :
Le seul nombre inférieur ou égal à![Rendered by QuickLaTeX.com \[p(B)=\dfrac{2}{6}=\dfrac{1}{3}\]](https://spe-maths.fr/wp-content/ql-cache/quicklatex.com-01feebe93f8cd971240eb4b1d3f0aa01_l3.png)
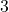 qui soit également un multiple de
qui soit également un multiple de 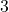 est
est 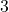 . Donc
. Donc 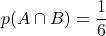 .
Ainsi:
.
Ainsi:
Les événements![Rendered by QuickLaTeX.com \[p(A)\times p(B)=\dfrac{1}{2}\times \dfrac{1}{3}=\dfrac{1}{6} =p(A\cap B)\]](https://spe-maths.fr/wp-content/ql-cache/quicklatex.com-5cb6aacbf9404a10494e1494983aba67_l3.png)
 et
et 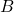 sont indépendants.
sont indépendants.
-
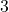 nombres sont pairs. Donc
nombres sont pairs. Donc
Les nombres inférieurs ou égaux à![Rendered by QuickLaTeX.com \[p(A)=\dfrac{3}{6}=\dfrac{1}{2}\]](https://spe-maths.fr/wp-content/ql-cache/quicklatex.com-ff63e9dfb75b8eebaf120d2611858488_l3.png)
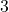 sont
sont 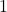 ,
,  et
et 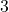 .
Donc :
.
Donc :
Le seul nombre pair inférieur ou égal à![Rendered by QuickLaTeX.com \[p(B)=\dfrac{3}{6}=\dfrac{1}{2}\]](https://spe-maths.fr/wp-content/ql-cache/quicklatex.com-d3793feebd5829437252cbf7fa6dc90c_l3.png)
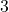 est
est  . Donc
. Donc 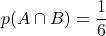 .
.
Les événements![Rendered by QuickLaTeX.com \[p(A)\times p(B)=\dfrac{1}{2}\times \dfrac{1}{2}=\dfrac{1}{4} \neq p(A\cap B)\]](https://spe-maths.fr/wp-content/ql-cache/quicklatex.com-a5444ce87c534dc88962e416bf5c04ac_l3.png)
 et
et 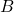 ne sont donc pas indépendants.
ne sont donc pas indépendants.
![]()
Exercice 6 ![]() Diagramme de Carroll
Diagramme de Carroll ![]()
Une maladie atteint ![]() d’une population de
d’une population de ![]() individus.
individus.
On appelle “malade” l’individu atteint de cette maladie et “bien portant” celui qui ne l’est pas.
On dispose d’un test pour la détecter.
Ce test donne les résultats suivants :
- Chez les individus malades,
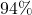 des tests sont positifs.
des tests sont positifs. - Chez les individus bien portants,
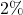 des tests sont positifs.
des tests sont positifs.
On note les événements suivants :
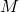 : “être malade”
: “être malade”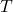 “avoir un test positif”
“avoir un test positif”
On rencontre une personne au hasard de cette population.
- Calculer
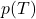 ,
, 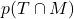 et
et 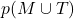 .
.

- Sachant que la personne rencontrée est malade, calculer la probabilité que son test soit négatif.

- Sachant que la personne rencontrée a un test positif, calculer la probabilité qu’elle ne soit pas malade.

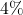 des
des 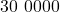 correspondent à
correspondent à 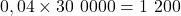 personnes malades.
personnes malades.
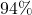 de
de 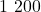 correspond à
correspond à 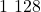 malades ayant un test positif.
malades ayant un test positif.
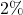 de
de 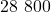 correspond à
correspond à 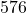 bien portants ayant un test positif.
bien portants ayant un test positif.
On peut ainsi construire le tableau suivant :
![Rendered by QuickLaTeX.com \[\begin{array}{|c|c|c|c|} \hline & \text{Malades} & \text{Bien portants} & \text{Total} \\\\ \hline \text{Test positif} & 1~128 & 576 & 1~704 \\\\ \hline \text{Test négatif} & 72 & 28~204 & 28~296 \\\\ \hline \text{Total} & 1~200 & 28~800 & 30~000 \\\\ \hline \end{array}\]](https://spe-maths.fr/wp-content/ql-cache/quicklatex.com-f1f9d805f05eec930b401a0137a24102_l3.png)

Ainsi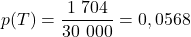
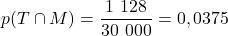
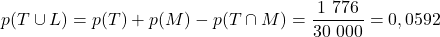

- La probabilité cherchée est
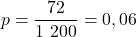

- La probabilité cherchée est
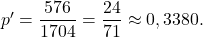
Le tableau ci-dessus s’appelle diagramme de Carroll [Lewis Carroll, mathématicien et écrivain britannique (1832-1898) qui a écrit le livre Alice au pays des merveilles]
c’est un tableau à double entrée dans lequel les éléments (ou effectifs, ou fréquences) d’un ensemble sont classés selon deux critères (l’un en ligne, l’autre en colonne) de façon à mettre en évidence les sous-ensembles qui constituent ces critères. Chaque région du diagramme contient alors les éléments qui ont les caractéristiques communes à la ligne et la colonne dont elle est l’intersection.
Exercice 7  Arbre de probabilité pondéré
Arbre de probabilité pondéré 
- Compléter l’arbre suivant :
- Déterminer la probabilité d’obtenir :
- 2 boules rouges
- 1 boule bleue et 1 boule rouge.
-
- D’après l’arbre pondéré, il y a un seul chemin qui réalise l’évènement « obtenir 2 boules rouges » c’est le chemin
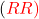

- Il y a deux chemins qui réalisent l’évènement » obtenir 1 boule bleue et 1 boule rouge » ce sont les chemins
 et
et  .
.
 .
.
Exercice 8  Arbre de probabilité pondéré
Arbre de probabilité pondéré 
1) Commencer par compléter l’arbre pondéré suivant, où on a noté les différents événements : F : «être femme», L : «porter des lunettes», H : «être homme».
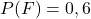 donc
donc 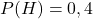 et la probabilité conditionnelle : probabilité de «porter des
lunettes» sachant que la personne est une femme est
et la probabilité conditionnelle : probabilité de «porter des
lunettes» sachant que la personne est une femme est 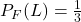 .
La probabilité conditionnelle: probabilité de «porter des lunettes» sachant que la personne est un homme est
.
La probabilité conditionnelle: probabilité de «porter des lunettes» sachant que la personne est un homme est 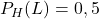 .
On peut donc compléter l’arbre pondéré.
.
On peut donc compléter l’arbre pondéré.
- On cherche la probabilité conditionnelle
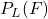 . On a :
. On a : 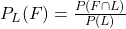 .
.
- D’une part :
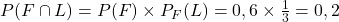 .
. - Et d’autre part, d’après la formule des probabilités totales on a :
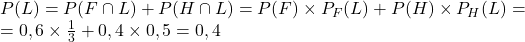 Donc :
Donc :
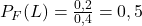
- D’une part :