Exercices sur les fonctions
Exercice 1 (Opérations sur les limites)
Calculer dans chacun des cas la limite demandée.
- $\lim\limits_{x \rightarrow 2^+} \frac{1}{x - 2} \quad \quad$ : Réponse $\color{red}{+\infty}$
$\quad$
- $\lim\limits_{x \rightarrow 1^+} \left(\left(5+\frac{1}{\sqrt{x-1}}\right) (2x+3)\right) \quad \quad$ : Réponse $\color{red}{+\infty}$
- $\lim\limits_{x \rightarrow 4^+} \frac{1-x}{x-4} \quad \quad$ : Réponse $\color{red}{-\infty}$
$\quad$
- $\lim\limits_{x \rightarrow 3^-} \frac{x^3-1}{3-x} \quad \quad$ : Réponse $\color{red}{+\infty}$
$\quad$
- $\lim\limits_{x \rightarrow +\infty} \frac{\sqrt{x+1}+\sqrt{x}}{x} \quad \quad$ : Réponse $\color{red}{0}$
- $\lim\limits_{x \rightarrow +\infty} \frac{x+1}{\sqrt{x}} \quad \quad$ : Réponse $\color{red}{+\infty}$
$\quad$
- $\lim\limits_{x \rightarrow -1^-} \frac{3x^2-5}{3x+3}\quad \quad$ : Réponse $\color{red}{+\infty}$
Pour des exercices corrigés type bac sur les fonctions , Cliquez ici |
Corrigé de l'exercice 1
- $\lim\limits_{x \rightarrow 2^+} (x -2) = 0^+$ donc $\lim\limits_{x \rightarrow 2^+} \frac{1}{x - 2} = +\infty$
- $\lim\limits_{x \rightarrow 1^+} \frac{1}{\sqrt{x-1}} =+\infty$
De plus $\lim\limits_{x \rightarrow 1^+} (2x+3) = 5$.
Par conséquent $\lim\limits_{x \rightarrow 1^+} \left(\left(5+\frac{1}{\sqrt{x-1}}\right) (2x+3)\right) = +\infty$
- $\lim\limits_{x \rightarrow 4^+} (1-x) = -3$ et $\lim\limits_{x \rightarrow 4^+} (x-4) = 0^+$ donc
$\lim\limits_{x \rightarrow 4^+} \frac{1-x}{x-4} = -\infty$
- $\lim\limits_{x \rightarrow 3^-}(x^3-1) = 26$ et $\lim\limits_{x \rightarrow 3^-} (3-x) = 0^+$ donc
$\lim\limits_{x \rightarrow 3^-} \frac{x^3-1}{3-x} = +\infty$
- $\frac{\sqrt{x+1} - \sqrt{x} }{x} = \sqrt{\frac{1}{x}+\frac{1}{x^2}}-\frac{1}{\sqrt{x}}$.
Or $\lim\limits_{x \rightarrow +\infty} \frac{1}{x} =\lim\limits_{x \rightarrow +\infty} \frac{1}{x^2} = 0$ et $\lim\limits_{x \rightarrow +\infty} \frac{1}{\sqrt{x}} = 0$
Donc $\lim\limits_{x \rightarrow +\infty} \frac{\sqrt{x+1} - \sqrt{x}}{x} = 0$
- $\frac{x+1}{\sqrt{x}} = \frac{x}{\sqrt{x}} + \frac{1}{\sqrt{x}}= \sqrt{x}+\frac{1}{\sqrt{x}}$.
Or $\lim\limits_{x \rightarrow +\infty} \sqrt{x}=+\infty$ et $\lim\limits_{x \rightarrow +\infty} \frac{1}{\sqrt{x}}=0$ Par conséquent $\lim\limits_{x \rightarrow +\infty} \frac{x+1}{\sqrt{x}}=+\infty$
- $\lim\limits_{x \rightarrow -1^-}(3x^2-5)= -2$ et $\lim\limits_{x \rightarrow -1^-} (3x + 3) = 0^-$
Donc $\lim\limits_{x \rightarrow -2^-} \frac{3x^2-5}{3x +3} = +\infty$
|
Exercice 2
A-Déterminer la limite à gauche et la limite à droite des fonctions suivantes en a.
1. 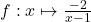 ;
; 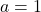 Réponse
Réponse 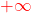 et
et 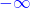
2. 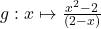 ;
; 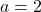 Réponse
Réponse  et
et 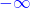
3. 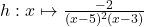 ;
; 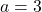 Réponse
Réponse  et
et 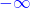
4. 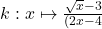 ;
; 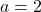 Réponse
Réponse  et
et 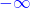
5.  ;
; 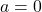 Réponse
Réponse  et
et 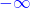
6. 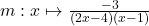 ;
; 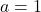 Réponse
Réponse  et
et 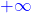
7. 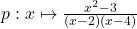 ;
; 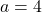 Réponse
Réponse  et
et 
B- Déterminer la limite des fonctions suivantes en a. « Forme indéterminée 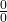 «
«
1. 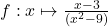 ;
; 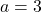 Réponse
Réponse 
2.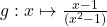 ;
; 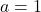 Réponse
Réponse 
3. 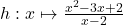 ;
; 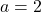 Réponse
Réponse 
4. 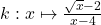 ;
; 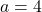 Réponse
Réponse 
Pour les limites suivantes utiliser la dérivation
5.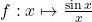 ;
; 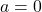 Réponse
Réponse 
6. 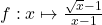 ;
;  Réponse
Réponse 
7. 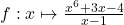 ;
; 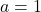 Réponse
Réponse 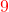
8. 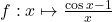 ;
; 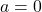 Réponse
Réponse 
Corrigé de l'exercice 2
A. Limite du type " $\color{blue} {\frac{\alpha}{0}}$" avec $\alpha \neq 0$
1. $\lim\limits_{x \to 1^-} (x-1) = 0^-$ donc $\lim\limits_{x \to 1^+} \frac{-2}{x - 1}=\color{red}{+\infty}$
et comme $\lim\limits_{x \to 1^+} (x-1) = 0^+$ alors $\lim\limits_{x \to 1^+} \frac{-2}{x - 1}=\color{blue}{-\infty}$
2. $\lim\limits_{x \to 2} (x^2-2) = 2$ et $\lim\limits_{x \to 2^-}(2-x)=0^+$ donc $\lim\limits_{x \to 2^-}\frac{x^2-2}{2 - x}=\color{red}{+\infty}$
et comme $\lim\limits_{x \to 2^+}(2-x)=0^-$ alors $\lim\limits_{x \to 2^+}\frac{x^2-2}{2 - x}=\color{blue}{-\infty}$
3. $\lim\limits_{x \to 3^-} (x - 5)^2(x - 3) = 0^-$ donc $\lim\limits_{x \to 3^+}\frac{-2}{(x - 5)^2(x - 3)}=\color{red}{+\infty}$
et $\lim\limits_{x \to 3^+} \frac{-2}{(x - 5)^2(x - 3)}=\color{blue}{-\infty}$
4. $\lim\limits_{x \to 2} (\sqrt{x} - 3) = \sqrt{2}-3 < 0$ et $\lim\limits_{x \to 2^-}(2x - 4)=0^-$ donc $\lim\limits_{x \to 2^-}\frac{\sqrt{x} - 3}{2x - 4}=\color{red}{+\infty}$ et $\lim\limits_{x \to 2^+}\frac{\sqrt{x} - 3}{2x - 4}=\color{blue}{-\infty}$
5. $\lim\limits_{x \to 0^-} x(x - 5)^2 = 0^-$ donc $\lim\limits_{x \to 0^-}\frac{-2}{x(x - 5)^2}=\color{red}{+\infty}$
et $\lim\limits_{x \to 0^+} \frac{-2}{x(x - 5)^2}=\color{blue}{-\infty}$
6. $\lim\limits_{x \to 1^-} (2x - 4)(x-1) = 0^+$ donc $\lim\limits_{x \to 1^-} \frac{ - 3}{(2x - 4)(x-1)}=\color{red}{-\infty}$
d'autre part $\lim\limits_{x \to 1^+}(2x - 4)(x-1)=0^-$ par conséquent $\lim\limits_{x \to 1^+} \frac{ - 3}{(2x - 4)(x-1)}=\color{blue}{+\infty}$
7. $\lim\limits_{x \to 4}(x^2- 3)=15$ et $\lim\limits_{x \to 4^-} ((x - 2)(x-4) = 0^-$ donc $\lim\limits_{x \to 4^-} \frac{ x^2- 3}{(x - 2)(x-4)}=\color{red}{-\infty}$
et comme $\lim\limits_{x \to 4^+}(2x - 4)(x-1)=0^+$ alors $\lim\limits_{x \to 4^+}\frac{ x^2- 3}{(x - 2)(x-4)}=\color{blue}{+\infty}$
|
B. Forme indéterminée" $\color{blue} {\frac{0}{0}}$"
1. Pour $x \neq 3$ ona $f(x) = \frac{x-3}{x^2-9} = \frac{x-3}{(x-3)(x+3)} = \frac{1}{x+3}$ donc $\lim\limits_{x \to 3}f(x)=\lim\limits_{x \to 3}\frac{1}{x+3}=\color{red}{\frac{1}{6}}$
2. Pour $x \neq 1 $ on a $g(x) = \frac{x-1}{(x-1)(x+1)} = \frac{1}{x+1}$ donc $\lim\limits_{x \to 1}g(x)=\lim\limits_{x \to 1}\frac{1}{x+1}=\color{red}{\frac{1}{2}}$
3. Pour $x \neq 2 $ on a $h(x) = \frac{(x-1)(x-2)}{x-2} = x-1 $ donc $\lim\limits_{x \to 2}h(x)=\lim\limits_{x \to 2}(x-1)=\color{red}{1}$
4. Pour $x > 0 $ et $x \neq 4$ on a $k(x) = \frac{\sqrt{x}-2}{(\sqrt{x}- 2)(\sqrt{x}+ 2)} = \frac{1}{\sqrt{x}+ 2} $ donc $\lim\limits_{x \to 4}k(x)=\lim\limits_{x \to 4}\frac{1}{\sqrt{x}+ 2} =\color{red}{\frac{1}{4}}$
Pour les limites suivantes on utilise la définition de la dérivée de la fonction $f$ en $a$ : $$\lim\limits_{x \to a}\frac{f(x) - f(a)}{x - a}=f'(a)$$
5.$\frac{\sin{x}}{x }=\frac{\sin{x}-0}{x-0 }=\frac{f(x)-f(0)}{x-0 }$ où $f(x)=\sin{x}$
La fonction $f$ est dérivable sur $\mathbb R$ donc en $0$ et sa dérivée est donnée par $f'(x)=\cos{x}$; $f'(0)=1$
comme $f$ est dérivable en $0$ $\lim\limits_{x \to 0}\frac{\sin{x}}{x }=\lim\limits_{x \to 0}\frac{\sin{x} - \sin{0} }{x - 0}=f'(0)=\color{red}{1}$.
6.$\frac{\sqrt{x}-1}{x-1 }=\frac{f(x)-f(1)}{x-1 }$ où $f(x)=\sqrt{x}$.
La fonction $f$ est dérivable sur $[0,+\infty$ donc en $1$ et sa dérivée est donnée par $f'(x)=\frac{1}{2\sqrt{x}}$; $f'(1)=\frac{1}{2}$
comme $f$ est dérivable en $1$ $\lim\limits_{x \to 1}\frac{\sqrt{x}-1}{x -1}=f'(1)=\color{red}{\frac{1}{2}}$.
7.Si on pose $f(x)=x^6+3x$ on a alors $f(1) = 1^6+3 =4$ et donc $$\frac{x^6+3x-4}{x-1}=\frac{f(x)-f(1)}{x-1 }$$
La fonction $f$ est dérivable sur $\mathbb R$ donc en $1$ et sa dérivée est donnée par $f'(x)=6x^5+3$; $f'(1)=9$
comme $f$ est dérivable en $1$, $\lim\limits_{x \to 1}\frac{(x^6+3x)-4}{x-1 }=f'(1)=\color{red}{9}$.
8.$\frac{\cos{x}-1}{x }=\frac{f(x)-f(0)}{x-0 }$ où $f(x)=\cos{x}$.
La fonction $f$ est dérivable sur $\mathbb R$ donc en $0$ et sa dérivée est donnée par $f'(x)=-\sin{x}$; $f'(0)=0$
comme $f$ est dérivable en $0$ $\lim\limits_{x \to 0}\frac{\cos{x}-1}{x }=f'(0)=\color{red}{0}$.
|
Exercice 3 (Limites dans le tableau de variations)
On donne le tableau de variations d’une fonction  :
:
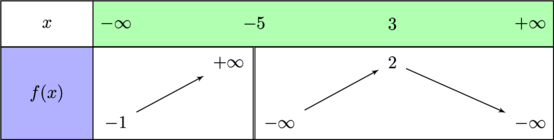
1) Déterminer les limites de  en
en  , en
, en 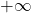 , en -5 à gauche et à droite.
, en -5 à gauche et à droite.
Corrigé de l'exercice 3
$\lim\limits_{x \to -\infty} f(x) = -1$
$\lim\limits_{x \to +\infty } f(x) = -\infty$
$\lim\limits_{x \to -5^-} f(x) = +\infty$
$\lim\limits_{x \to -5^+} f(x) = -\infty$
|
Exercice 4
On connaît le tableau de variations d’une fonction  :
:
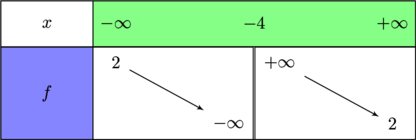
On sait de plus qu’il existe 2 réels  ,
, 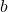 tels que
tels que  est définie sur
est définie sur 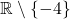 , par
, par 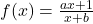 . Déterminer les valeurs de
. Déterminer les valeurs de  ,
, 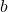 en justifiant.
en justifiant.
Corrigé de l'exercice 4
La fonction $f$ n'est pas définie en $x = -b$, donc $-b = -4$. Ainsi, $b = 4$.
Pour $x \neq 0$ on a $f(x) = \frac{ax+1}{x+b} = \frac{ax+1}{x+4} = \frac{ax(1+\frac{1}{ax})}{x(1+\frac{4}{x})} = \frac{a(1+\frac{1}{ax})}{(1+\frac{4}{x})}$. On en déduit les limites de $f$ en $ -\infty$ et $ +\infty$:
$\lim\limits_{x \to -\infty} f(x) = a$ et $\lim\limits_{x \to +\infty} f(x) = a $ et d'aprés le tableau de variation a= 2.
La fonction $f$ est donnée par $f(x)=\frac{2x+1}{x+4} $ |
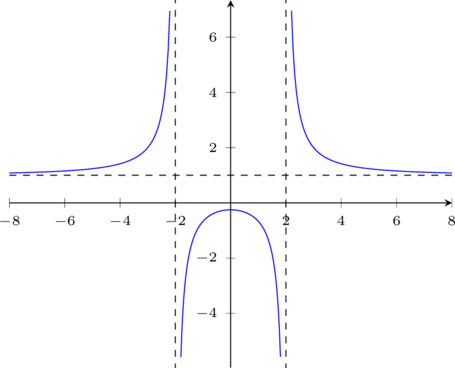
Exercice 5 (asymptotes horizontales et verticales)
On a tracé ci-dessous la courbe d’une fonction  définie sur
définie sur 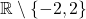 . Déterminer graphiquement les limites de
. Déterminer graphiquement les limites de  en
en  , en
, en  , en -2 et en 2 à droite et à gauche. Indiquer les asymptotes.
, en -2 et en 2 à droite et à gauche. Indiquer les asymptotes.
Corrigé de l'exercice 5
Asymptote horizontale d'équation $y=1$
- $\lim\limits_{x \to -\infty} f(x) = 1$
- $\lim\limits_{x \to +\infty } f(x) = 1$
Asymptotes verticales d'équations $x=-2$ et $x=2$
$\lim\limits_{x \to -2^-} f(x) = +\infty$
$\lim\limits_{x \to -2^+} f(x) = -\infty$
$\lim\limits_{x \to 2^-} f(x) = -\infty$
$\lim\limits_{x \to 2^+} f(x) = +\infty$
|
Exercice 6(QCM asymptotes)
Q1. Soit la fonction  définie sur
définie sur 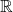 donnée par
donnée par 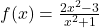 . La courbe
. La courbe 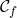 admet comme asymptote la droite d’équation :
admet comme asymptote la droite d’équation :
a. 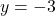 b.
b. 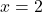 c.
c. 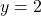 d.
d. 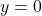
Q2. Soit la fonction 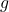 définie sur
définie sur 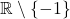 par
par 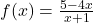 . La courbe
. La courbe  admet commes asymptotes :
admet commes asymptotes :
a. 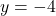 b.
b. 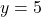 c.
c. 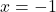 d.
d. 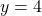
Corrigé de l'exercice 6
Q1: réponse c. (une asymptote horizontale)
Q2: réponse a. et réponse c. (une asymptote horizontale et une asymptote verticale ) |
Exercice 7
Soit $f$ la fonction définie sur $[1 ; 2]$ par $f(x)=x^{3}+x+5$.
Montrer que l'équation $f(x)=10$ admet une solution unique $\alpha$ sur $[1 ; 2]$, puis déterminer un encadrement de $\alpha$ d'amplitude 0,1 .
|
Corrigé de l'exercice 7
$f^{\prime}(x)=3 x^{2}+1 .$ Comme $x^{2} \geq 0$ alors $3 x^{2}+1 > 0$, $f'$ est strictement positif.
La fonction $f$ est continue et strictement croissante sur $[1 ; 2]$.
Or 10 est un nombre compris entre $f(1)=7$ et $f(2)=15$,
Donc, d'après le corollaire du théorème des valeurs intermédiaires, l'équation $f(x)=10$
admet une unique solution a sur $[1 ; 2]$.
On déterme un encadrement de $\alpha$ par essais successifs à l'aide de la calculatrice avec un pas de $0.1$ entre $1$ et $2$.
\begin{array}{|c|c|c|c|c|c|c|}
\hline x & 1 & ... & 1,5 & 1,6 & 1,7 & ... & 2\\
\hline f(x) &7 & ... & 9,88 & 10,70 & 11,61& ... & 15\\
\hline
\end{array}
Les valeurs de $f(x)$ sont arrondies à $10^{-2}$ près.
comme $f(\alpha)=10 \in [f(1.5),f(1.6)]$ alors $1,5 < \alpha <1,6$
L'encadrement cherché est: $1,5 < \alpha <1,6$. Et puisque $1,6-1,5=0,1$, l'amplitude est bien égale à 0,1 .
|
Exercice 8
- Démontrer que l'équation $2x^3−6x=6$ admet au moins une solution dans $\mathbb R$.
- Démontrer que l'équation $2x^3−6x=6$ admet exactement une solution $\alpha$ dans $\mathbb R$.
- Donner une valeur approchée de α à $10^{-2}$ près.
- Discuter, suivant les valeurs du réel $k$, le nombre de solution(s) de l'équation $2x^3−6x=k$.
|
Corrigé de l'exercice 8
- Posons $f(x)=2x^3−6x$. La fonction $f $ est définie sur $\mathbb R$. La figure suivante illustre la représentation graphique de $f$.

$f$ étant un polynôme elle est continue sur $\mathbb R$.
On a $f(2)=4$ et $f(3)=36$. Comme $6 \in [4,36]$ d'après le TVI, l'équation $f(x)=6$ admet au moins une solution dans $\mathbb R$.
- $f$ étant un polynome, $f$ est dérivable sur $\mathbb R$. Pour tout réel $x$, $f'(x)=6(x^2-1)$.
$f'(x) \geq 0$ pour $x \in ]-\infty,-1] \cup [1, +\infty[$ et $f'(x) < 0$ pour $x \in ]-1,1[$. On a $\lim\limits_{x \to -\infty}f(x)=-\infty$
et $\lim\limits_{x \to +\infty}f(x)=+\infty$, $f(-1)=4$ et $ f(1)=-4$ d'où le tableau de variation de $f$:

D'après le tableau de variation de $f$, l'équation $f(x)=6$ n'admet pas de solution dans l'intervalle $]-\infty,1]$ car $ \forall x \in ]-\infty,1], ~f(x) \leq 4$ et puisque $6 \in ]-4,+\infty[$ l'équation $f(x)=6$ admet exactement une solution dans l'intervalle $ [1,+\infty[$.
- D'après la représentation graphique de $f$,la solution $\alpha$ de l'equation $f(x)=6$ est proche de 2. Avec la calculatrice, on réalise un tableau de valeurs de $f$ en commençant par $x=2$ à $x=2,2$ par pas de 0,01. Voici une partie de ce tableau.
\begin{array} {|r|r|}\hline x & .... & 2,1 & 2,11 & 2,12 & ...\\ \hline f(x) & .... & 5,922 & 6,12786 & 6,336256 & .....\\ \hline \end{array}
On remarque que $2,1< \alpha < 2,11$. Pour plus de précision on refait un tableau de valeurs en commençant par $x=2$ avec un pas plus petit soit $0,001$.
\begin{array} {|r|r|}\hline x & 2,1 & 2,101 & 2,102 & 2,103 & 2,104 \\ \hline f(x) & 5,922 & 5,942472602 & 5,962970416 & 5,983493454 & 6,004041728 \\ \hline \end{array}
On voit que $2,103< \alpha < 2,104$. Donc $\alpha \approx{2,10}$ à $10^{-2} $ près.
D'après le tableau de variation de la fonction $f$ :

- si $k > 4$ l'équation $3x^3-6x=k$ admet une seul solution.
- Si $-4 < k < 4$ l'équation $3x^3-6x=k$ admet trois solutions
- Si $k=-4$ ou $ k= 4$ l'équation $3x^3-6x=k$ admet deux solutions.
|
Exercice 9
Simplifier l’écriture des expressions suivantes :
- $\ln (4e)$
$\ln e^3$
$\ln \left(\sqrt{e}\right)$
- $\ln \dfrac{1}{2} + \ln \dfrac{2}{5} + \ln \dfrac{5}{3} + \ln \dfrac{3}{2}$
- $\ln \left( 2 +\sqrt{2}\right)^{10} + \ln \left(2-\sqrt{2}\right)^{10}$
|
Corrigé de l'exercice 9
- $\ln (4e) = \ln 4 + \ln e=2\ln 2 + 1$;
$\quad \ln e^3 = 3\ln e = 3$;
$\quad \ln \left(\sqrt{e}\right) = \dfrac{1}{2} \ln e = \dfrac{1}{2}$. Donc
$\ln (4e) \ln e^3 \ln \left(\sqrt{e}\right) =
(2\ln 2 + 1)\frac{3}{2}$
- $\ln \dfrac{1}{2} + \ln \dfrac{2}{5} + \ln \dfrac{5}{3} + \ln \dfrac{3}{2}$ $=\ln 1-\ln 2 + \ln 2-\ln 5 + \ln 5-\ln 3 + \ln 3-\ln 2$ $= -\ln 2$ $\quad$ $\quad$
\begin{align*} \ln \left( 2 +\sqrt{2}\right)^{10} + \ln \left(2-\sqrt{2}\right)^{10}& = \ln \left( \left( 2 +\sqrt{2}\right)^{10} \times \left( 2 -\sqrt{2}\right)^{10} \right) \\\\ & = \ln \left(\left( 2 +\sqrt{2}\right)\left(2-\sqrt{2}\right)\right)^{10}\\\\ & = 10\ln\left(\left( 2 +\sqrt{2}\right)\left(2-\sqrt{2}\right)\right) \\\\ & = 10 \ln (4-2) \\\\ & = 10 \ln 2 \end{align*}
[/su_spoiler] |
Exercice 10
Résoudre les équations proposées après avoir fourni l’ensemble d’étude.
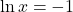
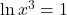
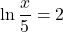
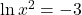
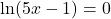
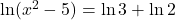
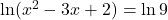
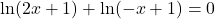
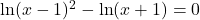
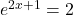
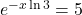
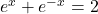
![]() ;
; ![]() Réponse
Réponse ![]() et
et ![]()
![]() ;
; ![]() Réponse
Réponse ![]() et
et ![]()
![]() ;
; ![]() Réponse
Réponse ![]() et
et ![]()
![]() ;
; ![]() Réponse
Réponse ![]() et
et ![]()
![]() ;
; ![]() Réponse
Réponse ![]() et
et ![]()
![]() ;
; ![]() Réponse
Réponse ![]() et
et ![]()
![]() ;
; ![]() Réponse
Réponse ![]() et
et ![]()
![]() «
« ![]() ;
; ![]() Réponse
Réponse ![]()
![]() ;
; ![]() Réponse
Réponse ![]()
![]() ;
; ![]() Réponse
Réponse ![]()
![]() ;
; ![]() Réponse
Réponse ![]()
![]() ;
; ![]() Réponse
Réponse ![]()
![]() ;
; ![]() Réponse
Réponse ![]()
![]() ;
; ![]() Réponse
Réponse ![]()
![]() ;
; ![]() Réponse
Réponse ![]()
![]() :
:
![]() en
en ![]() , en
, en ![]() , en -5 à gauche et à droite.
, en -5 à gauche et à droite.![]() :
:
![]() ,
, ![]() tels que
tels que ![]() est définie sur
est définie sur ![]() , par
, par ![]() . Déterminer les valeurs de
. Déterminer les valeurs de ![]() ,
, ![]() en justifiant.
en justifiant.![]() définie sur
définie sur ![]() . Déterminer graphiquement les limites de
. Déterminer graphiquement les limites de ![]() en
en ![]() , en
, en ![]() , en -2 et en 2 à droite et à gauche. Indiquer les asymptotes.
, en -2 et en 2 à droite et à gauche. Indiquer les asymptotes.
![]() définie sur
définie sur ![]() donnée par
donnée par ![]() . La courbe
. La courbe ![]() admet comme asymptote la droite d’équation :
admet comme asymptote la droite d’équation :![]() b.
b. ![]() c.
c. ![]() d.
d. ![]()
![]() définie sur
définie sur ![]() par
par ![]() . La courbe
. La courbe ![]() admet commes asymptotes :
admet commes asymptotes :![]() b.
b. ![]() c.
c. ![]() d.
d. ![]()
