Cours TRIGONOMÉTRIE
Exercice 1
La mesure principale d’un angle orienté est la mesure de cet
angle appartenant à l’intervalle ![Rendered by QuickLaTeX.com ]-\pi;\pi]](https://spe-maths.fr/wp-content/ql-cache/quicklatex.com-58de1f2d0fca5b7f795c1cba0b191771_l3.png) .
.
Exemple: L’angle orienté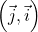 a plusieurs mesures:
a plusieurs mesures:
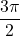 ,
, 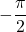 ,
,
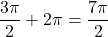 ,
,
Sa mesure principale est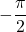 .
.
Déterminer la mesure principale des angles orientés suivants:
Exemple: L’angle orienté
Sa mesure principale est
Déterminer la mesure principale des angles orientés suivants:
Corrigé de l’exercice 2
Exercice 2
On souhaite résoudre l’équation suivante dans  :
:
![]()
- On effectue un changement de variable en posant
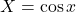 avec
avec ![Rendered by QuickLaTeX.com X\in[-1;1]](https://spe-maths.fr/wp-content/ql-cache/quicklatex.com-b5c5c57a192416a90ccb24e5460cd02c_l3.png) .
.
a. Quelle équation du second degré est équivalent à l’équation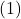 ?
?

b. Montrer que son discriminant peut s’écrire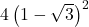 .
.

c. Déterminer les solutions de cette équation du second degré.

- En déduire les solutions de l’équation
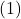 dans
dans ![Rendered by QuickLaTeX.com ]-\pi;\pi[](https://spe-maths.fr/wp-content/ql-cache/quicklatex.com-3db62912a9db4e1ba6bca4ca4c76e164_l3.png) puis dans
puis dans  .
.

Corrigé de l’exercice 2
- a. On pose
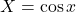 alors l’équation
alors l’équation  est équivalente à
est équivalente à ![Rendered by QuickLaTeX.com \[\begin{cases} X\in[-1;1] \\ 4X^2-2\left(1+\sqrt{3}\right)X+\sqrt{3}=0\end{cases}\]](https://spe-maths.fr/wp-content/ql-cache/quicklatex.com-2bb88dafef986d4f9e452619b1633abd_l3.png)

b. Le discriminant de l’équation du second degré est :

c.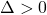
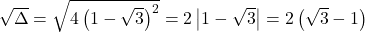
Il y a donc deux solutions réelles :
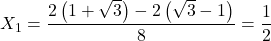
Et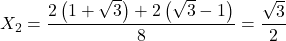

- On cherche donc les solutions dans
![Rendered by QuickLaTeX.com ]\pi;\pi]](https://spe-maths.fr/wp-content/ql-cache/quicklatex.com-0392010d97a2c65c52a293980a449a8e_l3.png) des équations
des équations 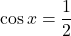 et
et 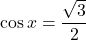 .
.
Les solutions sont donc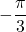 ,
, 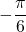 ,
, 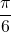 et
et 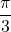 .
.

Sur , les solutions sont les nombres
, les solutions sont les nombres 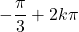 ,
, 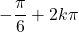 ,
, 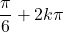 et
et 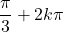 avec
avec 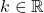 .
.