Cours VARIABLES ALÉATOIRES
Execice 1
Une compagnie d’assurance auto propose deux types de contrat :
Un contrat « Tous risques » dont le montant annuel est de 500 € ;
Un contrat « De base » dont le montant annuel est de 400 €.
En consultant le fichier clients de la compagnie, on recueille les données suivantes : 60 % des clients possèdent un véhicule récent ( moins de 5 ans ). Les autres clients ont un véhicule ancien ;
parmi les clients possédant un véhicule récent, 70 % ont souscrit au contrat « Tous risques » ;
parmi les clients possédant un véhicule ancien, 50 % ont souscrit au contrat « Tous risques ».
On considère un client choisi au hasard. D’une manière générale, la probabilité d’un événement est notée
est notée 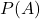 et son événement contraire est noté
et son événement contraire est noté 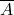 .
On note les événements suivants :
.
On note les événements suivants :
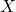 la variable aléatoire qui donne le montant du contrat souscrit par un client.
la variable aléatoire qui donne le montant du contrat souscrit par un client.
Un contrat « Tous risques » dont le montant annuel est de 500 € ;
Un contrat « De base » dont le montant annuel est de 400 €.
En consultant le fichier clients de la compagnie, on recueille les données suivantes : 60 % des clients possèdent un véhicule récent ( moins de 5 ans ). Les autres clients ont un véhicule ancien ;
parmi les clients possédant un véhicule récent, 70 % ont souscrit au contrat « Tous risques » ;
parmi les clients possédant un véhicule ancien, 50 % ont souscrit au contrat « Tous risques ».
On considère un client choisi au hasard. D’une manière générale, la probabilité d’un événement
-
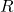 : « Le client possède un véhicule récent » ;
: « Le client possède un véhicule récent » ; 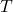 : « Le client a souscrit au contrat Tous risques ».
: « Le client a souscrit au contrat Tous risques ».
- Recopier et compléter l’arbre pondéré de probabilité traduisant les données de l’exercice.
- Calculer la probabilité qu’un client pris au hasard possède un véhicule récent et ait souscrit au contrat « Tous risques », c’est-à-dire calculer
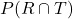 .
.
- Montrer que
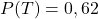 .
. - La variable aléatoire
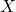 ne prend que deux valeurs
ne prend que deux valeurs  et
et 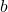 . Déterminer ces deux valeurs, les probabilités
. Déterminer ces deux valeurs, les probabilités 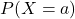 et
et 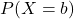 , puis l’espérance de
, puis l’espérance de 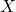 .
.