Calcul intégral avec Python
Exercice 14  Extrait Bac Métropole juin 2013, méthode des rectangles à gauche
Extrait Bac Métropole juin 2013, méthode des rectangles à gauche 
Soit ![]() la fonction définie sur
la fonction définie sur ![]() par
par ![]() . On note
. On note ![]() sa courbe représentative dans le plan muni d’un repère
sa courbe représentative dans le plan muni d’un repère ![]() . On pose
. On pose ![]() .
.
- interpréter géométriquement le réel
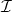
- On donne la fonction
 du programme python suivant :
du programme python suivant :

On note
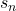 le nombre renvoyé par la fonction
le nombre renvoyé par la fonction  lorsqu’elle est appelé avec l’entier
lorsqu’elle est appelé avec l’entier  strictement positif.
Justifier que
strictement positif.
Justifier que 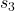 représente l’aire hachuré sur le graphique ci-dessous où les trois rectangles ont la même largeur.
représente l’aire hachuré sur le graphique ci-dessous où les trois rectangles ont la même largeur.

- Que dire de la valeur renvoyée par la fonction
 lorsque la valeur
lorsque la valeur  , lors de l’appel, devient grande?
, lors de l’appel, devient grande? - Écrire un programme Python qui utilise la fonction
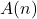 pour calculer une valeur approchée de
pour calculer une valeur approchée de 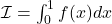 on donne la valeur exacte de
on donne la valeur exacte de 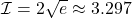 ,
,
-
Sur l’intervalle [0;1], la fonction
 est positive: le réel
est positive: le réel 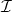 représente l’aire délimité par l’axe des abscisses la courbe
représente l’aire délimité par l’axe des abscisses la courbe 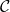 et les droites
et les droites 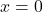 ,
, 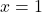 .
L’appel de la fonction pour
.
L’appel de la fonction pour - Lorsque n devient grand la valeur renvoyée par cet appel va converger vers la valeur de
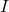 .
.
- Voici le programme Python qui calcul une valeur approché de
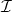 :
en affichant A(50), A(100),A(200),
:
en affichant A(50), A(100),A(200), on remarque que lorsque n devient grand
on remarque que lorsque n devient grand 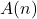 s’approche de la valeur de
s’approche de la valeur de 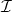 .
Remarque pour afficher
.
Remarque pour afficher
![]()
![]()
Exercice 15  méthode des rectangles à droite
méthode des rectangles à droite 
Soit ![]() la fonction définie sur
la fonction définie sur ![]() par
par ![]() . On note
. On note ![]() sa courbe représentative dans le plan muni d’un repère
sa courbe représentative dans le plan muni d’un repère ![]() . On pose
. On pose ![]() .
.
- interpréter géométriquement le réel
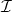
- On donne la fonction
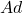 du programme python suivant :
du programme python suivant :

On note
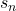 le nombre renvoyé par la fonction
le nombre renvoyé par la fonction  lorsqu’elle est appelé avec l’entier
lorsqu’elle est appelé avec l’entier  strictement positif.
Justifier que
strictement positif.
Justifier que 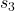 représente l’aire hachuré sur le graphique ci-dessous où les trois rectangles ont la même largeur.
représente l’aire hachuré sur le graphique ci-dessous où les trois rectangles ont la même largeur.

- Que dire de la valeur renvoyée par la fonction
 lorsque la valeur
lorsque la valeur  , lors de l’appel, devient grande?
, lors de l’appel, devient grande? - Écrire un programme Python qui utilise la fonction
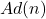 pour calculer une valeur approchée de
pour calculer une valeur approchée de 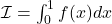 on donne la valeur exacte de
on donne la valeur exacte de 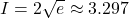 ,
,
- Comparer les valeurs de A(100) de l’exercice précédent, la valeur exacte de
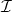 et Ad(100)
et Ad(100)
-
Sur l’intervalle [0;1], la fonction
 est positive: le réel
est positive: le réel 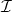 représente l’aire délimité par l’axe des abscisses la courbe
représente l’aire délimité par l’axe des abscisses la courbe 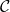 et les droites
et les droites 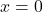 ,
, 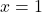 .
. - L’appel de la fonction pour
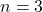 renvoie la valeur de
renvoie la valeur de
Le domaine hachuré sous la courbe de la figure se compose de 3 rectangles de largeur commune![Rendered by QuickLaTeX.com \[\frac{1}{3}f(\frac{1}{3})+\frac{1}{3}f(\frac{2}{3})+\frac{1}{3}f(1)\]](https://spe-maths.fr/wp-content/ql-cache/quicklatex.com-d2ea14738603dd0abdab20bdfc02226e_l3.png)
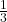 et de hauteurs respectives :
et de hauteurs respectives :
Donc l’aire de ce domaine est égale à![Rendered by QuickLaTeX.com \[f(\frac{1}{3});~f(\frac{2}{3});~f(1)\]](https://spe-maths.fr/wp-content/ql-cache/quicklatex.com-f965bf5a3e9ac929ae7f6cd756815dab_l3.png)
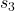 .
. - Lorsque n devient grand la valeur renvoyée par cet appel va converger vers la valeur de
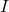 .
.
- Voici le programme Python qui calcul une valeur approché de
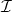 :
en affichant Ad(50), Ad(100),Ad(200),
:
en affichant Ad(50), Ad(100),Ad(200), on remarque que lorsque n devient grand
on remarque que lorsque n devient grand 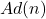 décroit en convergeant vers la valeur exacte de
décroit en convergeant vers la valeur exacte de 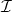 .
. -
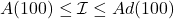
Exercice 16  Méthode de Monté-Carlo
Méthode de Monté-Carlo 
Soit ![]() la fonction définie sur
la fonction définie sur ![]() par
par ![]()
et ![]()
Dans un repère orthonormée on trace ![]() la courbe représentative de
la courbe représentative de ![]() sur
sur ![]() .
.
On choisit au hasard un point ![]() en tirant de façon indépendante ses coordonnées
en tirant de façon indépendante ses coordonnées
x et y dans l’intervalle ![]() .
.
on répète n fois cette expérience et on compte le nombre de point ![]() qui sont au-dessous de la courbe
qui sont au-dessous de la courbe ![]() .
.
La figure ci-dessous illustre ce processus pour ![]() .
.

Les disques noirs correspondent aux points sous la courbe, les disques blancs aux points au-dessus de la
courbe.
- Quelle est la condition que doivent vérifier les coordonnées du point M tiré au hasard pour qu’il soit sous la courbe
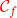 .
. - Que peut-on dire de la fréquence obtenue par le rapport du nombre de disques noirs sur le nombre total de disques, lorsque on augmente l’entier
 .
. - Exprimer la probabilité
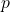 qu’un point tiré de cette manière soit situé sous la courbe
qu’un point tiré de cette manière soit situé sous la courbe 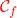 en fonction de
en fonction de 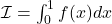 .
. - Compléter l’algorithme ci-dessous pour qu’il affiche la proportion
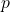 des points noirs dans le carré. L’instruction random() génère un nombre aléatoire compris entre 0 et 1 .
des points noirs dans le carré. L’instruction random() génère un nombre aléatoire compris entre 0 et 1 .

5. Ecrire un programme python qui donne une valeur approchée de ![]() .
.
- Le point
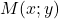 tiré au hasard est sous la courbe si
tiré au hasard est sous la courbe si 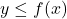 .
. - Quand
 augmente la fréquence des points sous la courbe s’approche de la probabilité qu’un point tiré au hasard soit situé sous la courbe.
augmente la fréquence des points sous la courbe s’approche de la probabilité qu’un point tiré au hasard soit situé sous la courbe. - Comme
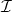 est l’aire de la partie inférieur du carré délimitée par la courbe et que l’aire total du carré est égale à 1, alors la probabilité
est l’aire de la partie inférieur du carré délimitée par la courbe et que l’aire total du carré est égale à 1, alors la probabilité 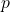 qu’un point tiré de cette manière soit situé sous la courbe est
qu’un point tiré de cette manière soit situé sous la courbe est 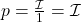 .
. - On complète la ligne 9 du programme par la condition qu’un point tiré soit sous la courbe: if y < = f(x): et à la ligne 10, on incrémente le compteur c de 1 : c=c+1.
- Voici le programme python qui donne une valeur approchée de
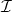 par la méthode Monté-Carlo. Afficher la valeur de I par l’instruction print I.
par la méthode Monté-Carlo. Afficher la valeur de I par l’instruction print I.
Remarque: La valeur exacte de cette intégrale est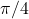 .
.
Ecrire un commentaire pour aider à améliorer le contenu