Rappel de cours
Séries entières d’une variable réelle ou complexe.
I-Séries entières d’une variable complexe
Définition 1. On appelle série entière toute série de fonctions de la forme 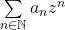 où
où 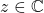 et
et 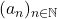 une suite de nombres complexes
.
une suite de nombres complexes
.
Définition 2. : 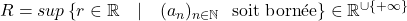 est appelé rayon de convergence de la série
est appelé rayon de convergence de la série 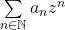 .
.
Proposition 1. On considère 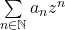 une série entière de rayon de convergence
une série entière de rayon de convergence 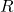 . Soit
. Soit  un élément de
un élément de 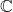 .
.
- Si
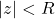 alors la série
alors la série 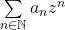 est absolument convergente,
est absolument convergente,
- si
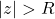 alors la série
alors la série 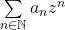 est divergente.
est divergente.
Détermination pratique du rayon de convergence.
Soit-
Règle de D’Alembert : Si
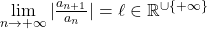 alors
alors 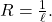
Règle de de Cauchy Si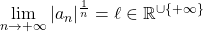 alors
alors 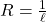 .
.
- Règle d’Hadamard: Si
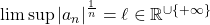 alors
alors 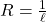 .
.
Propriétés de la somme d’une série entière
On désigne parExercice 1
Corrigé
Exercice 2